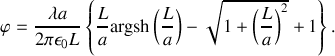Réponse 1
La notation proposée dans l'énoncé pour le potentiel créé au point
par un élément de longueur
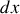de fil, est incomplète. Il faudrait en effet préciser en quel point
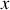l'élément de longueur est placé. Notons
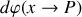la contribution au potentiel de l'élément de fil en question. Avec les notations de la figure 10,
Réponse 2
Le potentiel électrostatique est la somme de toutes les contributions élémentaires
:
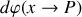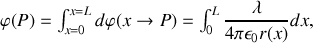
où
En posant
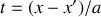, il vient
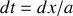et :
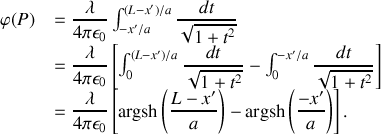
La fonction
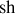étant impaire,
l'est aussi, d'où
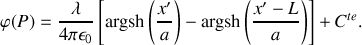
Il ne faut pas oublier la constante additive : seules les dérivées du potentiel ont un sens physique.
Réponse 3
Etant donné que pour
, la forme asymptotique de
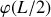pour
est
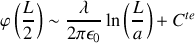
Réponse 4
Pour calculer le potentiel créé en dehors de son axe par un fil infiniment long, considérons un cylindre de même axe, de rayon
, hauteur
et appliquons le théorème de Gauss (nous calculons d'abord le champ électrique).
Attention :
n'a ici plus la même signification qu'aux questions précédentes :
désigne maintenant la distance au fil.
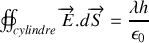
Le symbole
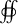désigne traditionnellement le flux d'un champ de vecteurs sur une surface fermée (ici, le cylindre). Le champ
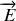n'a pas de composante suivant le fil car tout plan orthogonal au fil est plan de symétrie de la répartition de charges. De même, tout plan contenant le fil est plan de symétrie, d'où
en coordonnées cylindriques. Par ailleurs, le système est invariant par translation d'axe parallèle au fil, et par toute rotation dans un plan orthogonal au fil, d'où
. Ainsi,
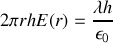
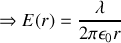
Le potentiel se déduit du champ par :
On obtient :
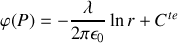
Si l'on choisit la constante de telle sorte que le potentiel s'annule à une distance
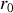du fil :
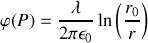
Dans la limite où
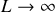, le potentiel trouvé à la question 3 doit tendre vers celui que nous venons de calculer. Mais dans cette limite l'expression de la question 3 diverge ! Pour pouvoir comparer les deux calculs, il faut reconsidérer le problème de la constante additive dans :
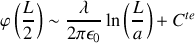
Pour être cohérent, il nous faut ici aussi choisir la constante de telle sorte que
ce qui donne,
qui est bien le potentiel régnant à la distance
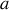d'un fil infini. Les résultats des questions 3 et 4 sont, sous cette forme, identiques.
Remarque :
La formule
n'est valable que pour des distributions de charges
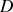d'extension finie. C'est ce qui explique que dans le cas du fil infini, nous avons d'abord calculé le champ électrique, duquel on a déduit le potentiel électrostatique. Pour obtenir le champ, nous avons utilisé le théorème de GAUSS qui est toujours valable, mais nous aurions pu aussi exploiter la relation
Contrairement à son analogue pour le potentiel, cette expression est valable même pour des distributions d'extension infinie, tant que la densité volumique de charge
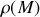est bornée. Cette différence tient à ce que :
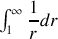est une intégrale impropre divergente
alors que :
est une intégrale impropre convergente.
Réponse 5
Dans un corps métallique supposé parfaitement conducteur (i.e. de conductivité ”infinie”), il ne peut exister de champ électrique (sinon, la densité volumique de courant serait infinie, en vertu de
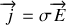). Or, en régime permanent,
, ce qui signifie que le potentiel est constant dans tout le volume et sur la surface d'un conducteur parfait.
Attention :
Il n'est pas possible que la charge surfacique du cylindre soit constante. Contrairement à la géométrie sphérique, la géométrie cylindrique ne permet pas d'avoir simultanément une charge surfacique constante et un potentiel constant. Les calculs justifiant cette affirmation sont lourds...
Réponse 6
Par hypothèse,
En posant
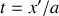, il vient :
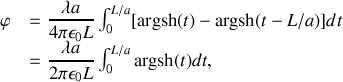
soit finalement,
