Le système, une mole de gaz parfait, est isolé matériellement dans un cylindre (A) de volume, V_A fermé par un piston \Pi. (A) peut communiquer par une conduite étroite avec un récipient rigide (B), mais cette conduite est obstruée par un robinet et (B) est initialement vide.
Le système est plongé dans un thermostat à 0°C, \Pi constitué par un mélange d'eau et de glace en équilibre. Par sa face supérieure, est mécaniquement en contact avec l'extérieur (opérateur), mais il en est thermiquement isolé.
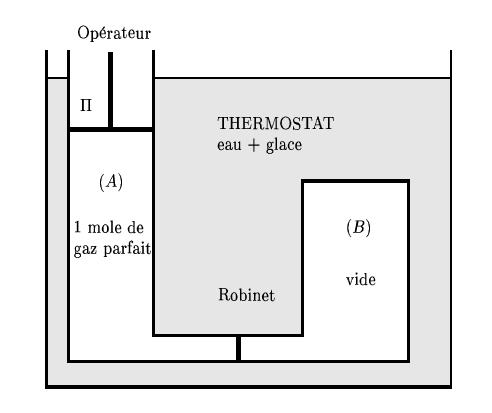
Pour chacune des questions, les conditions initiales sont les suivantes :
-
en B, le vide est total : P_B=0
-
en A, le gaz est à la pression P_A=P_o=0\cdot210^5 et occupe le volume V_A=V_o.
Question 1
Le robinet reste fermé. Un opérateur agit sur \Pi, et détend lentement le gaz jusqu'à la pression P_i=0\cdot368\, P_o. Calculer :
le travail W et la quantité de chaleur Q échangés par le gaz au cours de la transformation (on rappelle la valeur de la constante des gaz parfaits R=8\cdot31\, J\cdotmol^{-1}\cdotK^{-1}) ;
la masse m_1 de glace qui s'est formée dans le thermostat au cours de la transformation (chaleur latente de fusion de la glace : L_f=336\, kJ\cdotkg^{-1} \, à \, 0°C) ;
les variations d'entropie \DeltaS_1 du gaz et \DeltaS_{U1} de l'Univers. Commenter.
Question 2
On ouvre le robinet . \Pi reste immobile. On constate qu'après que le gaz a rempli (B), un nouvel équilibre s'établit à une pression P_2=0\cdot368P_o. Calculer :
le volume V_B;
les variations d'énergie interne, travail et chaleur échangés au cours de la détente ;
les variations d'entropie \DeltaS_2 du gaz et \DeltaS_{U2} de l'Univers. Commenter.
Question 3
On ouvre le robinet. Mais \Pi ne reste pas immobile ; l'opérateur le pousse lentement à mesure que le gaz s'échappe en (B) de manière à maintenir la pression dans (A) égale à . A la fin de l'opération, il n'y a plus de gaz en et sa pression dans (B) est P_3. Calculer :
la pression P_3 ;
le travail reçu par le gaz ;
la masse m_3 de glace qui a fondu dans le thermostat au cours de la transformation ;
les variations d'entropie \DeltaS_3 du gaz et \DeltaS_{U3} de l'Univers. Commenter.
Question 4
Le robinet reste fermé. Un opérateur agit sur \Pi, et comprime lentement le gaz. Or le gaz est en fait une mole de CCl_3F,dont la pression saturante à 0°C est P_S=0\cdot410^5Pa, proche de P_o. Aussi, une liquéfaction est très rapidement observée. L'opérateur continue de pousser le piston jusqu'à ce que le fluide soit entièrement liquide et n'occupe plus qu'un volume négligeable. Calculer :
le travail et la quantité de chaleur déjà échangés par le gaz au moment où la première goutte de liquide apparaît (point de rosée) ;
la masse m^a_4 de glace fondue dans le thermostat pendant cette première partie de la compression ;
le travail et la quantité de chaleur échangés entre le point de rosée et le point de liquide saturant, lorsque les dernières molécules de gaz se liquéfient (chaleur latente de vaporisation de CCl_3\, à \, 0°C : L_v=26\, kJ\cdotmol^{-1} ) ;
la masse m^b_4 de glace fondue pendant cette seconde partie de la compression.
Comparer m^a_4 et m^b_4, et conclure sachant que CCl_3F est un fluide réfrigérant couramment utilisé.