Le signe de se V_{AB} déduit de celui de Q_1 ou Q_2. Avec la convention d'orientation de la figure 8, la soudure \sigma_1est orientée en "récepteur" et la soudure \sigma_2 en "générateur". L'intensité qui traverse \sigma_1 de A vers B est i, d'où

Q_1=iV_{AB}(T_1)> 0 \quad où \quad V_{AB}= V_A - V_B.

De même, la soudure \sigma2 est traversée par une intensité i de B vers A et Q_2 devient :

Q_2=iV_{BA}(T_2) = -i V_{AB}(T_2)< 0.

En règle générale, V_{AB}(T) est donc du signe de i . Ainsi,

i>0 \quad \Rightarrow\quad V_{AB}(T)>0.

Nous supposerons dans la suite que est effectivement positif.

Par unité de temps, le thermocouple reçoit une quantité de chaleur Q_1 = i V_{AB}(T_1)>0 de la part de la source chaude, et il fournit une quantité de chaleur -Q_2 = iV_{AB}(T_2)>0 à la source froide.

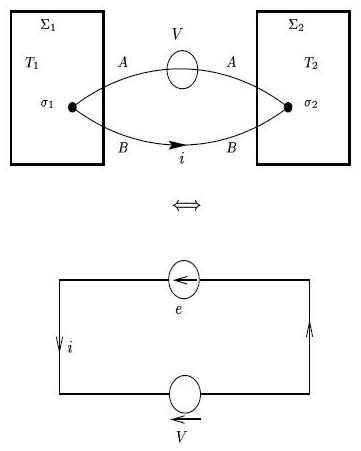
Choisissons d'orienter la force électromotrice e par la convention des générateurs (voir figure 9). Sur la figure, il faut considérer la force électromotrice e comme une représentation symbolique du thermocouple ; celle-ci est mesurée par le voltmètre V.

Par hypothèse, entre un instant et un instant t ultérieur quelconque, le système décrit un cycle. Cela signifie que le système reste toujours dans le même état et partant que toute fonction d'état reste constante, en particulier l'énergie interne U. Le premier principe prend alors une forme très simple :

W+Q_1+Q_2=0.

En d'autres termes,

-ei+i \, [V_{AB}(T_1)- V_{BA}(T_2)] = 0,

d'où

e= V_{AB}(T_1)-V_{AB}(T_2).

Pour calculer la variation d'entropie du système, nous pouvons utiliser

dS = \frac {\deltaQ}{T_{source}}

puisque les échanges de chaleur sont supposés réversibles. Il vient alors :

\DeltaS = i\frac {V_{AB}(T_1)}{T_1}-i\frac{V_{AB}(T_2)}{T_2].

Comme U, l'entropie est une fonction d'état et donc :

\DeltaS=0 entre deux instants quelconques.

Nous en déduisons la relation demandée entre les différences de potentiel et les températures :

\frac{V_{AB}\left(T_1\right)}{T_1} = \frac{V_{AB}\left(T_2\right)}{T_2}

et la force électromotrice devient :

e = V_{AB}\left(T_1)\, \left[\frac{T_1-T_2}{T_1}\right].

Si \Sigma_2 assimilable à un thermostat,

\frac{d}{dT_1}\, \left[ \frac {V_{AB}\left(T_1\right)}{T_1}\right] = \frac {D}{dT_1} \left[\frac{V_{AB}\left(T_2\right)}{T_2}\right] = 0.

En posant T=T_1, nous obtenons :

\frac {d}{dT} \, \left[\frac {V_{AB}\left(T_2\right)}{T_2}\right] = 0\qquad \Longrightarrow\qquad \frac{V_{AB}(T)}{T}= C^{te}

Soit \alpha la constante apparaissant dans l'expression précédente, il vient

V_{AB}(T) = \alphaT.

Comme V_{AB}(T) est positive, la constante \alpha est elle aussi positive.

L'expression de la force électromotrice devient :

e=\alpha(T_1-T_2) =\alpha\DeltaT.

Par conséquent,

\frac {de}{d(\DeltaT)}=\alpha>0.

Lorsqu'on augmente l'écart de température entre les deux soudures, on augmente de même la force électromotrice.

Le rendement est par définition le quotient du travail fourni à l'extérieur par unité de temps sur la chaleur reçue par le système par unité de temps,

\eta_0 = \frac{-W}{Q_1}.

Ainsi,

\eta_0 \frac{Q_1+Q_2}{Q_1} = 1 - \frac {V_{AB} \left(T_2\right)}{V_{AB}\left(T_1\right)},

ou encore,

\eta_0 = 1 - \frac{T_2}{T_1}.

Le rendement est donc égal au rendement de CARNOT, qui est le rendement maximal que peut atteindre un moteur ditherme fonctionnant entre les sources de chaleur \Sigma_1et \Sigma_2. En effet, puisque l'effet PELTIER est réversible, le "cycle" considéré l'est aussi. Effectuons un bilan entropique global :

\DeltaS_\mathrm{Univers} \quad = \quad \left{\begin{array}{cc} \DeltaS_\mathrm{thermocouple}\\ {0}\end{array}\right}\quad +\quad\left{\begin{array}{cc} \DeltaS_{\Sigma_1}\\ {-\frac{Q_1}{T_1} = -\alphai}\end{array}\right} \quad +\left{\begin{array}{cc} \DeltaS_{\Sigma_2}\\ {-\frac{Q_2}{T_2} = \alphai}\end{array}\right = \quad 0

La variation d'entropie de l' "Univers" est bien nulle.