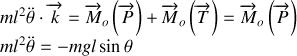Chute freinée d'un corps
Nous faisons l'hypothèse que le corps de masse
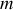 est freiné au cours de sa chute par une force de frottement de type visqueux. Nous étudions le problème dans un référentiel
est freiné au cours de sa chute par une force de frottement de type visqueux. Nous étudions le problème dans un référentiel
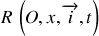 terrestre supposé galiléen. La chute se faisant sur un seul axe on se limite à un vecteur de base
terrestre supposé galiléen. La chute se faisant sur un seul axe on se limite à un vecteur de base
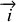 (figure 13). On supposera que la masse
(figure 13). On supposera que la masse
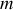 chute sans vitesse initiale d'une position
chute sans vitesse initiale d'une position
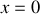 à
à
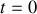 .
.
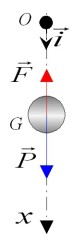
Nous étudions donc:
le système masse
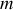
Référentiel
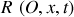 avec vecteur unitaire
avec vecteur unitaire
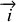
Forces extérieures appliquées :
Poids
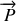 et force de frottement
et force de frottement
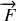
L'application de la relation fondamentale de la dynamique conduit à:
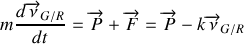
L'équation différentielle du mouvement de la masse
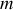 s'écrit donc:
s'écrit donc:
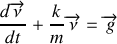
ce qui en projection sur l'axe
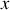 du mouvement conduit à:
du mouvement conduit à:
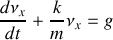
Cette équation est une équation différentielle du premier degré à coefficients et second membre constant. La méthode de résolution consiste à calculer une solution de l'équation sans second membre et d'y ajouter une solution particulière indépendante du temps. L'équation sans second membre s'écrit:
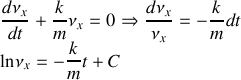
Il en résulte que la vitesse du mobile varie exponentiellement selon une loi du type:
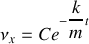
Une solution particulière de l'équation différentielle ne doit pas dépendre du temps. On a donc:
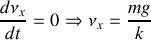
La solution générale de cette équation s'écrit donc:
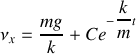
Il ne reste plus qu'à déterminer la constante
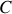 en revenant aux conditions aux limites de ce mouvement qui impose que
en revenant aux conditions aux limites de ce mouvement qui impose que
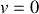 à
à
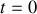 . Il vient donc:
. Il vient donc:
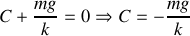
ce qui conduit à:
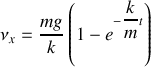
On peut ainsi constater que la vitesse augmente progressivement pour atteindre une vitesse limite lorsque le temps tend vers l'infini. La vitesse de chute qui logiquement n'est jamais atteinte est donnée par:
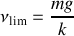
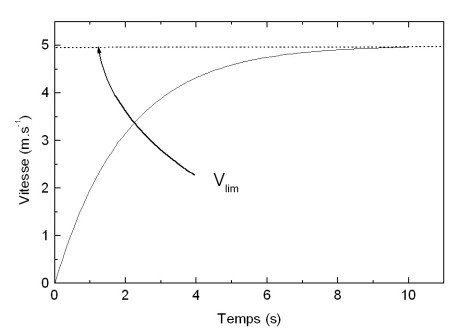
La position du mobile peut ensuite être déterminée par intégration de la vitesse ce qui conduit à:
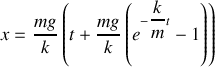
Pendule simple
Considérons une masse
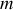 mobile autour d'un axe fixe. La distance de la masse
mobile autour d'un axe fixe. La distance de la masse
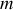 à l'axe de rotation est appelée
à l'axe de rotation est appelée
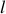 . On considère le mouvement du système masse
. On considère le mouvement du système masse
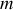 par rapport à un référentiel Galiléen
par rapport à un référentiel Galiléen
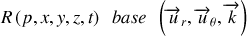 . La base choisie est la base mobile.
. La base choisie est la base mobile.
Les forces extérieures appliquées sont le poids
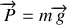 et la tension du fil
et la tension du fil
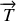 .
.
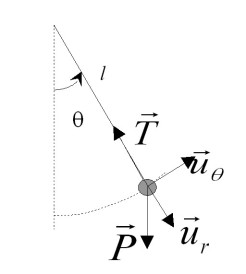
La relation fondamentale de la dynamique conduit à:
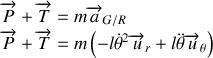
En projection sur les vecteurs de base, le poids et la tension s'écrivent :
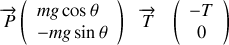
ce qui conduit à:
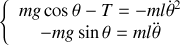
De la seconde équation, il est possible d'écrire l'équation différentielle du mouvement de la masse
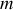 :
:
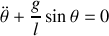
Cette équation est une équation différentielle non linéaire à cause de la présence du terme en sinus. La solution n'est donc pas facile à obtenir sauf si dans certaines conditions l'équation peut être assimilée à une équation linéaire. Cette condition est satisfaite dans le cas ou l'angle
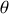 est petit c'est à dire lorsque le sinus est assimilable à l'angle, soit
est petit c'est à dire lorsque le sinus est assimilable à l'angle, soit
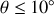 . Dans ce cas, l'équation différentielle devient:
. Dans ce cas, l'équation différentielle devient:
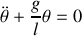
et la solution de cette équation s'écrit:
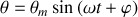
à condition de poser
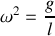
L'équation différentielle précédente aurait pu être obtenue directement par le théorème des moments calculés en
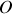 soit:
soit: