Nous introduisons maintenant une nouvelle fonction particulièrement utile dans tous les problèmes de mécanique que l'on appelle l'énergie mécanique d'un système. Nous partons pour définir cette fonction du théorème de l'énergie cinétique dans lequel nous faisons apparaître le travail des forces conservatives et celui des forces non conservatives soit :
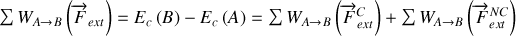
En appelant
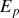l'énergie potentielle totale, somme des énergies potentielles dont dérive chaque force conservative, on peut écrire :
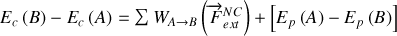
ce qui se transforme en changeant l'énergie potentielle de membre en
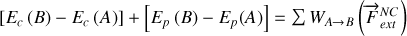
Si l'on regroupe dans le premier membre les fonctions qui ne dépendent que de
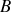et de
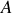il vient:
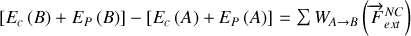
Il est possible d'introduire une nouvelle fonction d'état appelée énergie mécanique
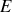du système en posant
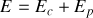
L'introduction de cette fonction permet de présenter de façon très simple le bilan énergétique d'un système par la relation suivante :
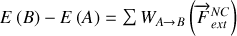
ce qui conduit au théorème de l'énergie mécanique :
Théorème :
La variation d'énergie mécanique d'un système entre deux points
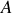et
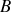est égale à la somme des travaux des forces non conservatives appliquées au système entre ces deux points
Remarque :
Les forces non conservatives étant des forces résistantes l'énergie mécanique d'un système ne peut que diminuer au cours du temps.
Complément :
Cependant lorsqu'un système est mécaniquement isolé, (c'est à dire pour un système qui ne subit aucune force extérieure non conservative), l'énergie mécanique se conserve. L'énergie mécanique ne dépend plus du point considéré.
