Définition de la stabilité
Pour un système soumis uniquement à une force conservative, il est intéressant de savoir s'il existe des états d'équilibre ou pas. La forme locale de l'énergie potentielle permet d'écrire que :
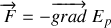
Dans le cas où l'énergie potentielle ne dépend que d'une variable
, cela revient à dire que :
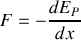
La condition d'équilibre se traduisant par
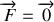peut donc s'écrire aussi
.
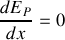Une position d'équilibre se traduit donc par un extremum de la fonction énergie potentielle.
Remarque :
Un équilibre est dit stable si, à la suite d'une perturbation qui a éloigné le système de cette position, celui-ci y retourne spontanément. Dans le cas contraire l'équilibre est dit instable.
Conditions de la stabilité
Reprenons le cas où l'énergie potentielle ne dépend que d'une variable
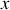et supposons que pour
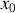la dérivée de cette fonction est nulle. Pour une perturbation amenant le système à
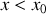, la valeur algébrique de la force doit être positive pour ramener le système vers
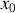soit
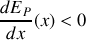. Dans le cas contraire
, la force doit être négative et donc
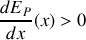(voir l'exemple de la masse accrochée à un ressort de la figure 22). La fonction
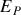décroît avant
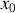et est croissante après
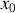. Elle présente donc un minimum pour
.
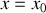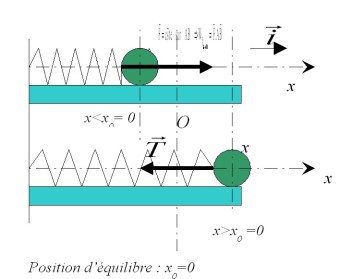
Figure 22 : Évolution de la masse vars sa position d'équilibre
. Pour
, la valeur algébrique
de la tension est positive alors que pour
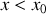elle est négative.
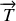est une force de rappel.
Dans ce cas, la fonction
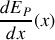est une fonction croissante qui s'annule pour
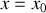. La condition de stabilité, c'est à dire
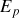minimale, peut donc se traduire par
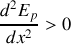au voisinage de
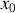et donc pour
.
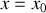Dans le cas contraire, la position sera une position d'équilibre instable.
Attention :
Equilibre stable pour
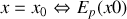minimale
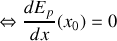et
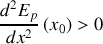
Equilibre instable pour
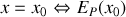maximale
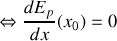et
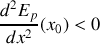
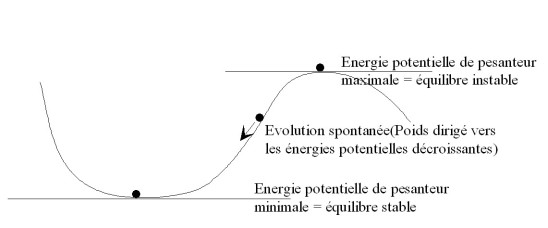
Un système, livré à lui-même, évolue donc spontanément vers un état d'équilibre qui correspond à une position pour laquelle l'énergie potentielle est minimale.
Remarque :
On peut écrire :
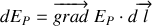avec
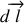vecteur déplacement élémentaire quelconque.
Pour un déplacement sur une surface d'énergie potentielle constante,
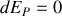. Le vecteur
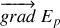est donc perpendiculaire aux surfaces d'égale énergie potentielle.
Pour un déplacement perpendiculaire aux surfaces équipotentielles, vers les énergies potentielles croissantes,
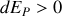et donc
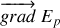à la même direction que le déplacement. Le vecteur
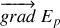est donc dirigé vers les énergies potentielles croissantes.
La force
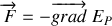est donc toujours dirigée vers les énergies potentielles décroissantes.
Attention :
Un système, livré à lui-même, évolue spontanément vers les énergies potentielles décroissantes.
Ce que nous venons de formuler peut s'illustrer simplement par l'exemple suivant. Considérons une bille de masse
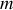pouvant se déplacer sur un sol constitué d'un creux et d'une bosse. L'énergie potentielle de pesanteur de cette masse ne peut varier qu'entre une valeur maximale (sommet de la bosse) et une valeur minimale (fond du creux).
