On appelle oscillateur harmonique tout système dont le paramètre ou degré de liberté
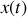peut se mettre sous la forme:
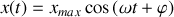
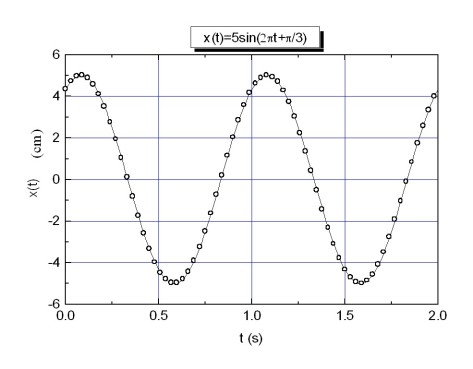
La figure 1 montre l'allure de l'évolution du paramètre
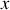en fonction du temps
.
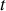Par définition nous appellerons
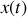l'élongation (ou la position) à l'instant
,
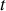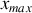l'élongation maximale ou l'amplitude,
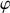la phase à l'origine,
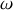la pulsation du mouvement et
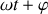la phase à l'instant
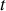. La position d'un oscillateur harmonique de fréquence
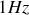, d'amplitude
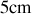est représentée sur la figure 1.
La période T des oscillations
La période
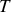des oscillations est le temps mis par l'oscillateur pour revenir à une position identique quelque soit le choix de cette position. Mathématiquement la période
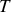est définie par:
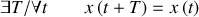
Cette relation montre que la période est un nombre
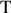qui doit être indépendant de la date
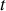choisie pour la définir.
Remarque :
Il est courant de représenter la position d'un oscillateur par un nombre complexe ou de façon équivalente par la représentation de Fresnel. En effet, nous voyons que, ce qui définit la position de l'oscillateur c'est l'association de son amplitude
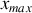et de sa phase
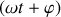à l'instant
.
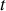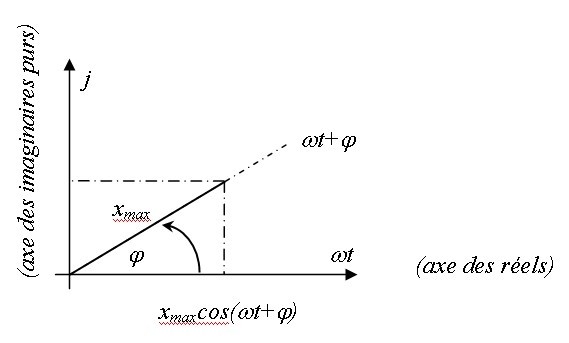
La position instantanée
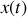de l'oscillateur est donnée par la partie réelle du nombre complexe
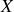défini par:
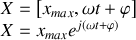
Par abus d'écriture , il est fréquent de confondre le nombre complexe
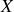avec la position instantanée
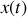de l'oscillateur. On écrit ainsi que:
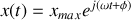
ce qui n'a pas de sens physique mais qui est bien pratique du point de vue scriptural.
Vitesse instantanée de l'oscillateur
La vitesse instantanée de l'oscillateur est alors donnée par:
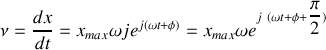
On constate que la vitesse est déphasée de
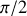par rapport à la position. Cela montre bien que, lorsque l'oscillateur passe par l'origine
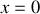, sa vitesse est maximale alors que, quand il passe par son élongation maximale
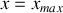, sa vitesse est nulle.
Accélération de l'oscillateur
De même on peut calculer l'accélération de l'oscillateur:
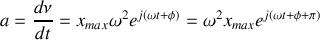
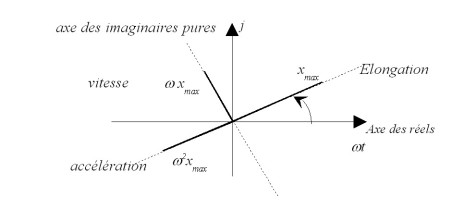
Cette relation montre que l'accélération de l'oscillateur est en opposition de phase avec l'amplitude. La représentation dans le plan complexe de ces trois grandeurs est présentée sur la figure 3.
