De la relation précédente, il est facile de voir que l'accélération de l'oscillateur est liée à sa position par la relation:
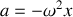
Il en résulte que l'équation différentielle du mouvement d'un oscillateur harmonique est donnée par:
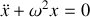
Tout système dont l'équation différentielle du mouvement est de cette forme est un oscillateur harmonique ce qui peut se résumer de la façon suivante:
Oscillateur harmonique
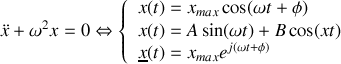
Remarque :
Il est utile de noter que la forme de la solution de l'équation différentielle peut être écrite de différentes façons mais que si l'écriture diffère (voir ci-dessus) la solution
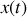reste la même. La somme d'un sinus et d'un cosinus affectés d'amplitudes
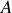et
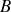est bien équivalente à un cosinus affecté d'une certaine phase. La dernière forme
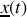est la solution dans l'espace des complexes. Seule la partie réelle
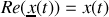correspond à la solution physique de l'équation différentielle.
