Le mouvement d'un oscillateur, qu'il soit amorti ou non, est en général appréhendé de façon classique en représentant l'évolution de son élongation en fonction du temps. Ce traitement classique utilisé dans les paragraphes précédents est justifié par la nature déterministe du mouvement de l'oscillateur et par le fait que l'équation différentielle du mouvement est linéaire.
Rappel :
L'équation est dite linéaire car si
est solution de cette équation, il en va de même pour
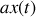avec
. Le mouvement des oscillateurs que nous avons étudiés précédemment est régi (sauf dans le cas du frottement solide) par l'équation différentielle suivante
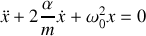
L'oscillateur est amorti si
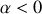et entretenu si
. Ce dernier cas n'est pas fréquent en mécanique car les frottements fluides imposent
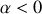. Toutefois il est possible de réaliser des oscillations entretenues avec des dispositifs électroniques.
L'équation précédente peut se réécrire
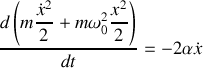
L'équation ci-dessus n'est rien d'autre que la traduction énergétique de l'équation différentielle du mouvement. En particulier nous voyons que dans le cas d'un oscillateur harmonique pour lequel
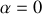, la quantité
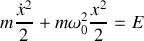
se conserve.
Remarque :
Nous voyons ainsi apparaître que si l'on porte sur un graphe la position de l'oscillateur en abscisse et en ordonnée sa vitesse, nous obtenons une ellipse qui définit ce que l'on appelle le portrait de phase de l'oscillateur. L'équation ci-dessus est en effet de la forme
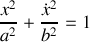
à condition de poser
