Pour un oscillateur harmonique le portrait de phase est une ellipse (figure 14). L'ellipse se répète indéfiniment dans le temps ce qui est une signature de la conservation de l'énergie de l'oscillateur.
Remarque :
L'ellipse peut être parcourue dans un sens ou dans un autre ce qui montre que le mouvement est invariant par renversement du temps.
Attention :
Pour un oscillateur harmonique donné il est clair que le portrait de phase ne dépend que de l'énergie mécanique
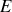de l'oscillateur.
Attention :
Pour une oscillateur amorti, l'énergie ne se conserve plus et diminue au cours du temps. L'amplitude des oscillations décroît exponentiellement au cours du temps ainsi que la vitesse. Le portrait de phase est alors caractérisé par une spirale logarithmique dont le centre
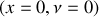porte le nom d'attracteur (figure 15).
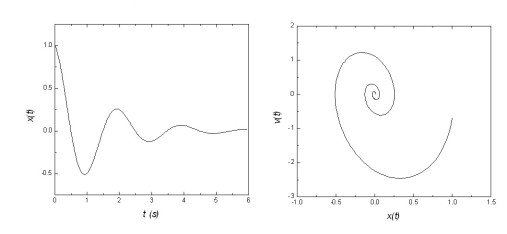
Il n'est pas indifférent de parcourir la spirale dans un sens ou dans l'autre ce qui montre bien que le mouvement n'est plus invariant par renversement du temps. Il est clair en effet que le frottement engendre inéluctablement l'irréversibilité du mouvement.
