La résolution d'un problème de mécanique requière la plupart du temps l'utilisation d'une équation fondamentale qui puisse s'appliquer un tout point du solide. Puisque ce cours s'intéresse spécifiquement au domaine élastique des déformations, nous proposons ici d'utiliser les lois de comportement mises en place dans le chapitre précédent pour établir l'équation fondamentale de l'élastostatique, dite équation de Lamé-Clapeyron.
Considérant un système solide de volume ![]() délimité par la surface
délimité par la surface ![]() , l'équation fondamentale de la statique s'exprime :
, l'équation fondamentale de la statique s'exprime :
où ![]() et
et ![]() sont respectivement les forces volumique et surfacique. La force surfacique correspond à la contrainte s'exerçant sur un élément de surface
sont respectivement les forces volumique et surfacique. La force surfacique correspond à la contrainte s'exerçant sur un élément de surface ![]() de normale
de normale ![]() , d'où :
, d'où :
Le théorème d'Ostrogradsky permet alors de transformer l'intégrale de surface en une intégrale de volume :
L'équation fondamentale de la statique peut donc se réécrire :
qui devient naturellement une équation locale, vérifiable en tout point du solide :
Par projection sur les trois axes d'un repère orthonormé, on obtient :
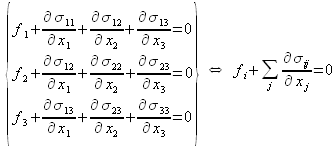
Selon la loi de comportement déjà établie entre le tenseur des contraintes et le tenseur des déformations, on peut développer le gradient de ![]() :
:
où ![]() et d'autre part :
et d'autre part :

soit :
Par conséquent, on a :
et le gradient du tenseur des contraintes se développe comme :
La forme locale de l'équation fondamentale s'écrit alors :
constituant l'équation fondamentale de l'élastostatique, encore appelée équation de Lamé-Clapeyron.
En notation indicielle, cette équation s'écrit :
La résolution d'un problème d'élasticité consiste alors à résoudre cette équation à laquelle il convient d'adjoindre les conditions aux limites.
Une approche différente peut néanmoins être utilisée. Il s'agira alors de déterminer les contraintes s'exerçant sur le système et d'en déduire les déformations subies à l'aide de la loi de comportement élastique :
Il est toutefois nécessaire de s'assurer que les composantes du tenseur des déformations obtenues présentent les propriétés d'un tenseur des déformations pures ; autrement dit, il doit exister un champ de déplacement ![]() vérifiant, pour chacun des éléments tensoriels, que
vérifiant, pour chacun des éléments tensoriels, que ![]() . Cette nécessité introduit de fait des conditions portant sur les contraintes ; en plus des conditions aux limites, on doit alors vérifier les 6 équations suivantes, communément appelées
. Cette nécessité introduit de fait des conditions portant sur les contraintes ; en plus des conditions aux limites, on doit alors vérifier les 6 équations suivantes, communément appelées « conditions de Beltrami »
:
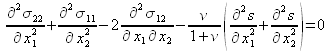

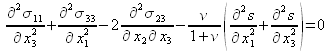
Remarque :
Les trois premières relations se déduisent les unes des autres par permutation circulaire des indices. Il en est de même pour les trois dernières relations.



