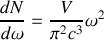Soit une boite cubique de dimension a dont les parois sont entièrement réfléchissantes. On suppose, en outre, qu'il n'existe pas de sources duc champ électromagnétique. Un champ électromagnétique à l'intérieur de la cavité est caractérisé par un potentiel vecteur
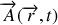qui obéit à l'équation de d'Alembert :
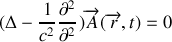
En considérant la dépendance de la forme
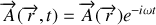, on obtient :
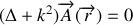
L'espace à l'intérieur de la cavité étant exempte de charges, d'où la jauge de Coulomb :
.
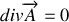Ceci est équivalent à la transversalité des ondes planes (
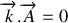). Un système d'ondes stationnaires s'établit à l'intérieur de la cavité avec le vecteur potentiel de la forme :
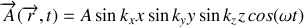
On impose aux parois d'être parfaitement réfléchissantes (composantes tangentielles nulles ) :
;
;
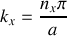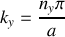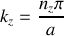
Les indices
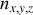sont des entiers positifs.
Il y a autant de vecteurs potentiels que de triplets (
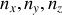) (modes).
Dans un espace à trois dimensions chaque mode est représenté par un point (exemple à deux dimensions) :
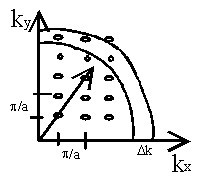
Le nombre de modes entre
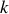et
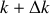est :
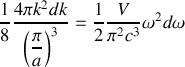
Si de plus on tient compte des deux directions de polarisation de chaque mode, la densité des modes est :
