Définition :
Dans un référentiel inertiel
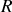, l'équation régissant le mouvement d'une particule de charge
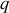en présence d'un champ électrique constant
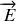et/ou d'un champ magnétique constant
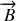est connue sous le nom de force de Lorentz :
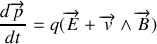
Remarque :
Le quadrivecteur impulsion est lié au quadrivecteur vitesse qui se ré-écrit
:
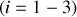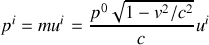
c'est-à-dire
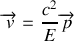
Exemple :
A titre d'application, traitons dans le référentiel
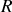, le mouvement d'une particule dans un champ électrique constant lorsque la vitesse initiale
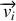est perpendiculaire à
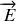. Les données initiales sont :
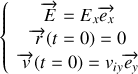
Traitons le problème avec l'approche relativiste. L'intégration de l'équation associée à la force de Lorentz donne :
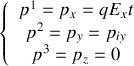
La quatrième composante du quadrivecteur impulsion,
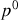, s'obtient à partir de la relation énergie-impulsion :
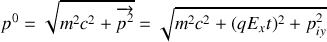
En faisant usage de la relation entre
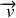et
, on obtient :
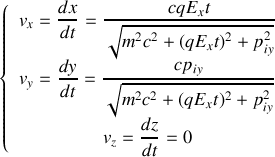
Ces équations mettent déjà bien en évidence l'effet relativiste. En effet, classiquement on écrirait :
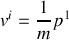, donc
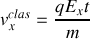et
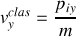. En particulier,
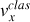croît linéairement avec le temps : elle atteint la vitesse de la lumière après un temps
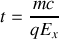, puis la dépasse ! Par contre, dans les relations obtenues, lorsque
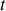tend vers l'infini, la vitesse tend vers
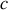. L'équation de la trajectoire demande quelques calculs. Avec l'approche relativiste on obtient :
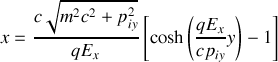
Cette expression se réduit à une parabole à la limite classique.
Pour conclure, disons que l'électrodynamique relativiste des particules chargées en présence de champs électrique et magnétique est indispensable pour comprendre le fonctionnement des accélérateurs de particules ou des microscopes électroniques, dans lesquels les vitesses sont relativistes.
