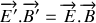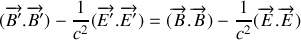Que deviennent les champs électriques et magnétiques dans un référentiel
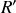? Deux approches sont possibles. Dans la première, la plus générale, il faut d'abord établir les formules de transformations pour les champs électrique et magnétique, ainsi que pour la charge
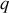. Cette opération (hors programme) est non triviale car les vecteurs
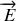et
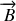sont fonctions, via les équations de Maxwell des quadrivecteurs associés aux grandeurs i) potentiel scalaire
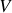et potentiel vecteur
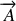qui forment le quadrivecteur
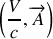et ii) densité de charge électrique
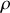et densité de courant
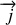qui forment le quadrivecteur
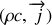. Rigoureusement, il faut former un tenseur (une matrice) d'éléments
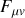et de dimension 4x4, dans lequel figurent les composantes
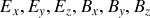. Aussi on fera l'hypothèse que la charge électrique
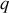d'une particule est invariante par changement de référentiel inertiel (analogie avec la masse
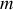d'une particule).
Fondamental :
Dans la seconde approche, on considère l'équation associée à la force de Lorentz. les composantes spatiales de l'impulsion appartiennent au quadrivecteur impulsion. En relativité, comme en mécanique classique, on associe une force à la dérivée par rapport au temps d'une quantité de mouvement. On introduit donc un quadrivecteur force, dont les composantes
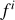sont définies par la relation :
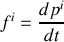
Les composantes associée à la force de Lorentz sont
.
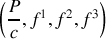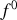est associée à la puissance
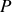de la somme des forces qui s'exercent sur la particule. Le quadrivecteur force se transforme, lors d'un changement de référentiel inertiel, à l'aide des transformations de Lorentz.
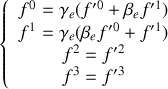
Il suffit ensuite d'introduire les champs électrique et magnétique. Les calculs, longs mais sans réelle difficulté, permettent d'obtenir les relations qui lient les composantes des champs
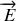et
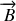suite à une transformation de Lorentz. Ainsi, on obtient :
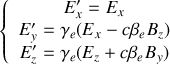
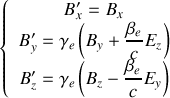
Ces lois sont très particulières. En effet, les composantes longitudinales des deux champs sont inchangées par la transformation de Lorentz, alors que les composantes transverses se mélangent. Par exemple, si pour un observateur inertiel
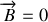, un autre observateur inertiel verra aussi bien
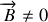que
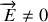. On peut vérifier que deux grandeurs sont invariantes :
