Ces boucles de courant élémentaires ne sont autres que les électrons circulant autour des noyaux des atomes.
Considérons l'atome de Bohr, formé d'un électron de masse
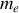 et de charge
et de charge
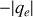 en orbite circulaire autour d'un proton supposé fixe. L'orbite de cet électron est parcourue en une période
en orbite circulaire autour d'un proton supposé fixe. L'orbite de cet électron est parcourue en une période
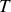 , l'intensité électrique correspondante vaut donc
, l'intensité électrique correspondante vaut donc
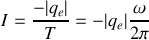 avec
avec
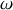 la vitesse angulaire de l'électron.
la vitesse angulaire de l'électron.
D'après la définition du moment magnétique créé par cette boucle de courant de surface
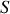
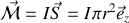
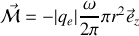
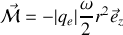
Si nous considérons le moment cinétique orbital
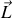 de l'électron
de l'électron
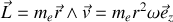
par conséquent
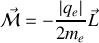
Expérimentalement, pour un système réel, on relie
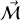 à
à
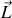 par la relation
par la relation
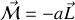 où
où
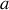 est le rapport gyromagnétique
est le rapport gyromagnétique
Remarque :
L'approximation de l'atome de Bohr n'est jamais totalement vraie pour diverses raisons liées à la mécanique quantique, aux couplages divers, au fait que les atomes ont plusieurs électrons, et
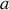 diffère de façon plus ou moins grande de
diffère de façon plus ou moins grande de
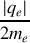 suivant la complexité du système étudié.
suivant la complexité du système étudié.
Une conséquence de cette relation est l'effet Einstein-de Haas : en modifiant l'aimantation d'un système, on peut modifier son moment cinétique et donc le mettre en mouvement.
D'autre part, dans le modèle de l'atome de Bohr, le moment cinétique orbital de l'électron est quantifié suivant
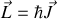
avec
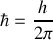 la constante de Planck qui vaut
la constante de Planck qui vaut
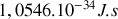 (voir le cours de physique quantique).
(voir le cours de physique quantique).
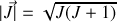
avec
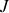 un nombre entier ou demi-entier (d'où la notion de quantification de l'énergie).
un nombre entier ou demi-entier (d'où la notion de quantification de l'énergie).
Définition :
On appelle la quantité
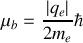 le magnéton de Bohr.
le magnéton de Bohr.
On introduit ainsi le facteur de Landé
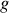 tel que :
tel que :
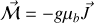
et on constate que
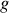 varie entre 1 et 2 suivant la nature du système considéré.
varie entre 1 et 2 suivant la nature du système considéré.
En particulier, l'électron lui-même possède un moment cinétique intrinsèque de rotation sur lui-même (dit "spin") pour lequel
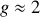 (loin du résultat classique).
(loin du résultat classique).
D'autre part, si on applique au matériau un champ magnétique
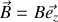 , alors en notant
, alors en notant
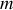 le nombre quantique magnétique
le nombre quantique magnétique
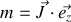
suivant l'état du système
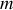 ne pourra prendre que
ne pourra prendre que
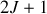 valeurs entre
valeurs entre
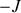 et
et
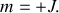
Par conséquent l'énergie d'interaction du système avec le champ magnétique qui vaut
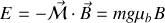 sera elle-même quantifiée.
sera elle-même quantifiée.
Remarque :
On voit apparaître dans ce cas une influence de
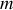 sur l'énergie du système alors qu'en l'absence de champ magnétique ce nombre quantique n'a pas d'influence (levée de dégénérescence par effet Zeeman).
sur l'énergie du système alors qu'en l'absence de champ magnétique ce nombre quantique n'a pas d'influence (levée de dégénérescence par effet Zeeman).



