Nous venons de calculer l'amplitude diffractée par une fente simple d'épaisseur 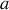selon l'axe des 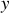. Nous avions trouvé

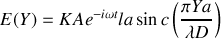
avec 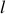largeur du faisceau incident.

Nous allons procéder au calcul de l'amplitude diffractée par un cheveu de même épaisseur. Nous supposerons qu'il est parfaitement opaque et qu'il est éclairé par une onde plane de section carrée d'arête finie 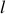. Il s'ensuit que

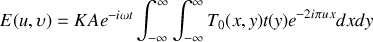
ou 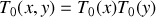définit la fonction délimitant le faisceau incident. Cette fonction est nulle si on ne se trouve pas dans le faisceau et est égale à 1 dans le cas contraire. La fonction 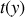définit la fonction de transparence du cheveu. Elle vaut 0 sur le cheveu et 1 dans le cas contraire. Il s'ensuit que

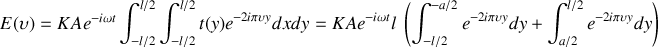
On obtient donc

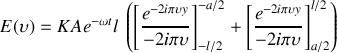
soit

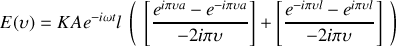
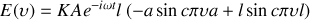
Le champ est donc la somme de deux termes. Le premier terme est l'opposé de celui créé par la fente et le second est lié à la contribution du faisceau direct. Le faisceau étant bien plus large que le cheveu ce terme est concentré en 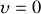.Si l'on omet cette partie là de la figure de diffraction nous pouvons conclure que :

la figure de diffraction créée par deux ouvertures complémentaires est identique sauf au centre de la figure

ce qui constitue le théorème de Babinet.