Pour l'équilibre d'un système isolé, il est nécessaire et suffisant que, pour tous les changements possibles de l'état d'un système qui ne modifient pas son énergie, la variation de son entropie soit nulle ou négative ; que dans tous les changements d'état où son entropie ne varie pas, la variation de son énergie soit nulle ou positive. (1)
[Il existe] deux formes d'énergie, l'énergie libre et l'énergie liée. (...) [D]ans un système dont la température est maintenue uniforme et constante, les réactions qui commencent d'elles-mêmes et continuent sans le secours d'aucun travail externe ne peuvent se produire que dans le sens où l'énergie libre diminue. (2)
_____________________________________________________________________________________________
À certains égards, le principe de conservation de l'énergie est une définition de l'énergie. L'énergie est la grandeur physique qui se conserve dans un système isolé et dans l'Univers. C'est une intégrale première des équations différentielles qui régissent l'évolution des systèmes. En thermodynamique, plusieurs fonctions d'état peuvent lui être associées, selon les variables d'état les mieux adaptées à la description du système physique considéré. En particulier pour un système divariant, il existe plusieurs choix possibles des deux paramètres d'état qui permettent de le décrire. Ainsi, comme le montre la relation thermodynamique fondamentale,
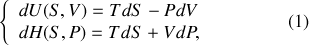
le choix de l'entropie
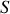et du volume
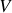est-il celui de l'énergie interne
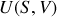tandis que le choix de
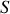et de la pression
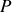est celui de l'enthalpie
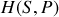. Cela peut être également être déduit de l'écriture différentielle du premier principe, selon que l'on considère les travaux volumétrique
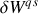ou technique
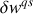échangeables par le système au cours d'une transformation quasistatique (qs) :
Rappel :
Le travail technique quasi-statique différentiel
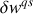est défini par la quantité
.
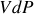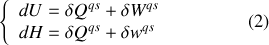
Il est remarquable que l'on puisse passer de l'énergie interne à l'enthalpie par simple ajout de la fonction d'état que constitue le produit
:
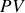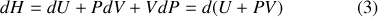
Cette opération mathématique, qui permet d'intervertir le rôle des paramètres
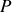et
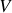dans l'expression différentielle, est nommée « transformation de Legendre »
. Comme l'énergie est définie par deux paires de paramètres d'état associés, les couples thermique
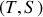et mécanique
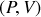, il existe une autre transformation de Legendre. En soustrayant le produit
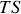(« énergie liée »
) à l'énergie interne et à l'enthalpie, on obtient deux nouvelles fonctions d'état permettant de caractériser l'énergie, l'énergie libre
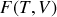et l'enthalpie libre
:
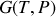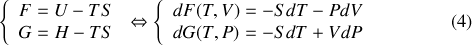
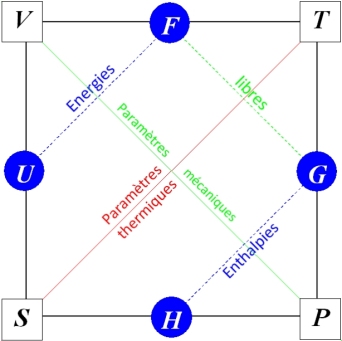
Ainsi présentées, les transformations de Legendre paraissent un simple jeu formel que synthétise le carré de Max Born représenté à la figure 1. En réalité, elles facilitent l'étude du système en autorisant un choix de paramètres d'état adapté à son environnement. Elles permettent surtout de généraliser le second principe à des systèmes qui ne sont pas nécessairement isolés. Ce n'est donc pas un hasard si elles doivent leurs noms et/ou les lettres qui les désignent symboliquement aux grands physiciens qui ont jeté les bases de la thermodynamique ou l'ont perfectionné : Clausius (énergie interne
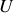), Helmholtz (énergie libre
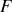), Willard Gibbs (enthalpie libre
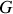) et Kamerlingh Onnes (enthalpie
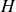) (3).
Le but de ce cours est de mettre en lumière l'utilité des fonctions thermodynamiques associées au principe de conservation de l'énergie. Cette utilité ne se limite pas au choix des variables thermodynamiques les plus adaptées. Ces fonctions sont en effet des « potentiels thermodynamiques »
prenant des valeurs minimales à l'équilibre. De plus, elles permettent de définir mathématiquement tous les « coefficients thermiques »
d'un système. Enfin, elles conduisent au « potentiel chimique »
, fonction cruciale pour la compréhension des systèmes ouverts, des transitions de phase et des réactions chimiques.
