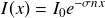1. Calcul différentiel
Considérons une "tranche" de matériau d'épaisseur infinitésimale dx. Nous allons calculer la variation infinitésimale de l'intensité du faisceau dI dans cette petite tranche dx.
InformationsPour cela, calculons tout d'abord le nombre d'événements (c'est-à-dire de réactions)
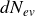se produisant par seconde dans cette tranche dx. Le nombre de noyaux par unité se surface (nombre de noyaux par centimètre carré) dans cette tranche est :
En utilisant la relation démontrée précédemment, on peut donc écrire :
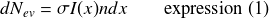
L'analyse en dimensions de cette équation permet de vérifier sa cohérence.
2. Lien entre nombre d'événements et intensité
Le nombre de réactions
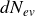se produisant (par unité de temps) est égal en valeur absolue au nombre de particules du faisceau qui sont absorbées (par unité de temps) :
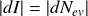
Ceci correspond à une diminution de l'intensité du faisceau, c'est-à-dire :
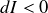
Donc :
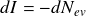
En reprenant l'expression (1) :
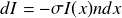
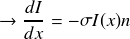
3. Résolution de l'équation différentielle
Nous venons d'obtenir :
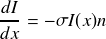
On intègre cette relation différentielle afin d'obtenir la loi d'évolution de I(x) :
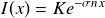avec K constante réelle (relation (1)).
Conditions initiales :
A l'entrée de la cible, c'est-à-dire à
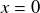, l'intensité vaut
.
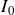On écrit l'équation à
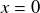pour déterminer la valeur de la constante K :
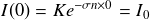
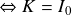
En remplaçant dans la relation (1) on obtient la loi d'atténuation :
|
