On considère un réseau comprenant des dipôles actifs et passifs et on s'intéresse au fonctionnement d'un dipôle
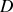 particulier. Il est traversé par un courant
particulier. Il est traversé par un courant
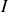 et la d.d.p. entre ses bornes est
et la d.d.p. entre ses bornes est
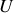 .
.
Supposons que
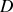 soit isolé du reste du réseau. Si ce reste de réseau est actif, la f.e.m. mesurée entre
soit isolé du reste du réseau. Si ce reste de réseau est actif, la f.e.m. mesurée entre
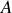 et
et
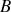 vaut
vaut
 : c'est la tension en circuit ouvert. S'il est rendu passif c'est-à-dire si les générateurs sont remplacés par leurs résistances internes, la résistance mesurée entre
: c'est la tension en circuit ouvert. S'il est rendu passif c'est-à-dire si les générateurs sont remplacés par leurs résistances internes, la résistance mesurée entre
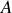 et
et
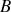 vaut
vaut
 . On remplace
. On remplace
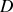 par une source de tension idéale de f.e.m.
par une source de tension idéale de f.e.m.
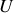 . D'après le théorème de superposition, le fonctionnement du circuit est inchangé. Le courant
. D'après le théorème de superposition, le fonctionnement du circuit est inchangé. Le courant
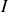 est la superposition d'un courant
est la superposition d'un courant
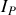 correspondant à la passivation de toutes les sources autres que
correspondant à la passivation de toutes les sources autres que
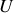 et d'un courant
et d'un courant
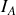 où seule la source
où seule la source
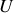 est passivée :
est passivée :
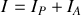
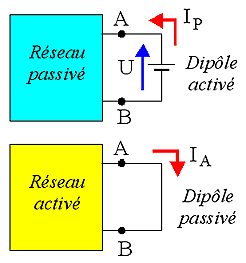
Si le générateur qui remplace
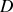 est seul à être actif le reste du réseau est équivalent à
est seul à être actif le reste du réseau est équivalent à
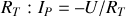
Si on passive ce générateur, il est équivalent à une résistance nulle : le reste du réseau débite dans ce fil le courant
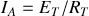
Ce courant est le courant de court-circuit entre
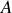 et
et
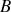 .
.

L'équation du circuit équivalent est donc :
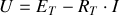
Cette équation est celle d'un générateur de tension que l'on nomme le générateur de
Thévenin
du circuit. Les deux circuits de la figure 19 sont équivalents et l'application de la loi de Pouillet au circuit de droite donne de façon triviale :
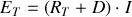
Remarque :
Un réseau linéaire, vu entre deux bornes
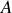 et
et
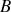 , peut être remplacé par un générateur de tension de f.e.m.
, peut être remplacé par un générateur de tension de f.e.m.
 et de résistance interne
et de résistance interne
 .
.
 est la d.d.p. mesurée à vide entre
est la d.d.p. mesurée à vide entre
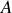 et
et
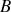 .
.
 est la résistance mesurée entre A et
est la résistance mesurée entre A et
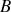 quand
quand
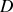 est retiré du circuit et que tous les générateurs du réseau sont remplacés par leurs résistances internes.
est retiré du circuit et que tous les générateurs du réseau sont remplacés par leurs résistances internes.





