Attention :
On se limitera ici à l'étude des signaux sinusoïdaux. Toutes les grandeurs sont complexes et fonction de
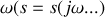. La tension à la sortie du mélangeur est :
.
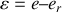Soit
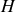la fonction de transfert ou gain en « boucle ouverte » de la chaîne d'action.
La tension de sortie est :
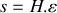
S'il n'y a pas de réaction :
S'il y a réaction :
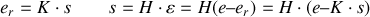
On en déduit :
.
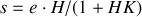Si l'on pose
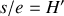, on tire la relation connue sous le nom de formule de Black.
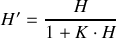
Réaction positive
Si
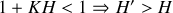. La réaction est positive.
Un système à réaction positive est instable : quand le signal d'entrée croît, la croissance du signal de sortie induit une nouvelle augmentation du signal d'entrée : le signal de sortie diverge jusqu'à ce que la saturation ou le blocage viennent limiter son amplitude.
Cas particulier
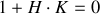
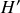est alors infini : on obtient un système oscillateur qui fournit un signal de sortie en l'absence de signal d'entrée. Pour obtenir un oscillateur stable, il faut trouver une méthode qui rende le produit
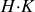rigoureusement égal à
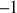une fois que les oscillations sont déclenchées. Cette condition est nommée « critère de Barkhausen ».
Réaction négative
Si
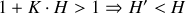. La réaction est négative. A priori il n'y a pas de problèmes de stabilité. Nous allons examiner les conséquences de la contre-réaction sur le fonctionnement des circuits.
Cas particulier
Le gain du système bouclé devient alors
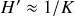. Le gain ne dépend plus de la chaîne d'action mais seulement de la chaîne de contre-réaction. Si la réponse de celle-ci est linéaire, la réponse du système bouclé est linéaire.
