Contre-réaction en tension
Le signal est appliqué sur l'entrée +. Sur l'entrée inverseuse, et donc en opposition de phase avec le signal d'entrée, on envoie la fraction \beta\cdotVs du signal de sortie. Avec un réseau de réaction passif, on a : V_s=\mu\cdotv_E=\mu\cdot\left(V_E-\beta\cdotV_S \right) \Rightarrow V_S=\mu\cdotV_E/(1+\mu\cdot\beta)
Si \mu est très grand devant \beta, la fonction de transfert devient :
V_s /V_E=1/\beta
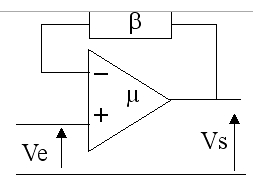
Si le gain en boucle ouverte est très supérieur à celui de la boucle de contre-réaction, alors le gain en tension du système bouclé ne dépend que du gain de cette boucle de rétroaction.
Les performances du système bouclé deviennent alors indépendantes de celles de l'amplificateur.
Contre-réaction en courant
La sortie est bouclée sur l'entrée inverseuse par une résistance R_2 : V_S = \mu\cdot(V_{E2} – V_A).
Le courant d'entrée en A dans l'amplificateur opérationnel étant très faible (< 1\muA) est négligeable devant celui qui circule dans R_1 et R_2.
V_A – V_{E1} = R_1\cdoti = R_{1}\cdot(V_S – V_{E1})/(R_1 + R_2)
On pose : \beta=R_1/(R_1+R_2)
V_A – V_{E1} = \beta\cdot(V_S – V_{E1}) \,\,\,\Rightarrow \,\,\,V_A = \beta\cdotV_S + (1 – \beta)\cdotV_{E1}
Or V_S = \mu\cdot(V_{E2} – V_A)
V_S = \mu\cdotV_{E2} – \mu\beta \cdotV_S – \mu\cdot(1 – \beta)\cdotV_{E1}
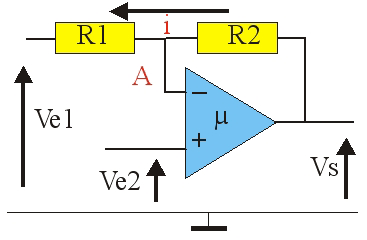
V_s=\frac{\mu}{1+\mu\beta }\left((V_{E2}-V_{E1}(1-\beta)\right) \qquad\qquad (1)
Si le gain \mu est infini, l'expression de la tension de sortie devient :
V_S = \left[V_{E2} – V_{E1}\cdot(1 – \beta)\right] /\beta