-
Le gain de l'amplificateur opérationnel est fini et fonction de la fréquence du signal. Le gain du système ne dépend pas uniquement de la boucle de réaction.
-
L'amplificateur contient des générateurs de tension et de courant parasites qui modifient la tension de sortie.
-
La bande passante est limitée et dépend du gain du système bouclé.
-
L'amplificateur ne peut délivrer en sortie qu'une puissance limitée.
Du fait de ces imperfections, le fonctionnement d'un amplificateur réel diffère de celui d'un amplificateur idéal dans un certain nombre de domaines.
Problèmes liés à la valeur finie du gain
L'expression du gain est donnée par : V_s=\frac{\mu}{1+\mu\beta}\left((V_{E2}-V_{E1}(1-\beta)\right)
Si on suppose que : \mu=\infty\RightarrowV_S={V_{E2}-V_{E1}\cdot(1-\beta)} /\beta
On introduit ainsi une erreur relative : \epsilon=(V'_S-V_S)/V_S=1/\mu\cdot\beta
On utilise le multiplicateur inverseur de la figure 7\cdot (V_{E2} = 0)
On prend : R_1 = 10 k\Omega et \,R_2 = 100 k\Omega.
Dans le modèle idéal, on a : A_V = V_S /V_{E1} = – 10 \, et \,\beta = 1/11.
Si \mu=1000, on commet une erreur \epsilon = 1/\mu\cdot\beta = 11 \cdot 10^{–3} = 1,1%
Problèmes liés aux tensions d'offset
A cause des imperfections des amplificateurs opérationnels, la tension de sortie n'est pas nulle quand les deux entrées sont au même potentiel. Si ce phénomène présente un inconvénient, on peut le corriger en introduisant un déséquilibre de l'amplificateur, ajustable de l'extérieur, afin d'obtenir une tension nulle en sortie lorsque les deux entrées sont placées au même potentiel.
Problèmes d'offset liés aux courants d'entrée
En fait les courants d'entrée I_{B1} et I_{B2} ne sont pas nuls et de plus ils ne sont pas identiques pour les deux entrées. Considérons le circuit de la figure 5 ; si l'amplificateur opérationnel est idéal, sa tension de sortie est nulle.
Soit V_S la tension de sortie de l'amplificateur réel. V^+ = – R_3\cdotI_{B2}; I_1 = I_0 + I_{B1}, donc :
(V_S – V^–)/R_2 = V^–/R_1 + I_{B1}
V_S\cdotR_1 – V^–\cdotR_1 – V^–\cdotR_2 = I_{B1}\cdotR_1\cdotR_2
V_S = I_{B1}\cdotR_2 + V^–\cdot(R_1 + R_2)/R_1
Mais pour l'amplificateur on a : V^+ = V^–
V_S = I_{B1}\cdotR_2 – \{(R_1 + R_2)/R_1\cdot\}R_3\cdotI_{B2}
On peut minimiser la valeur de la tension de sortie parasite V_S en faisant : R_3 = R_1\cdotR_2/(R_1 + R_2).
R_3 = (R_1 // R_2). C'est également l'impédance vue par l'entrée – de l'amplificateur.
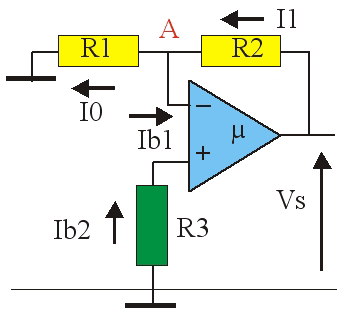
Pour minimiser l'influence des courants d'offset il faut placer des impédances identiques sur chaque entrée.
Réponse en fréquence
On peut, en première approximation, considérer que les amplificateurs opérationnels réels se comportent comme des systèmes du premier ordre ayant une fréquence de coupure inférieure voisine de 10 Hz et dont le produit GB gain-bande passante en système bouclé est constant.
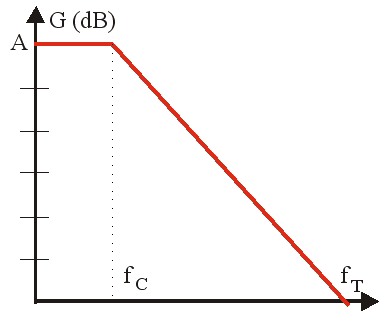
En première approximation, le gain s'écrit :
\mu=\frac{A}{1+j\cdotf/f_c \qquad\qquad (3)
A est le gain en continu et f_C la fréquence de coupure. Au-delà de f_C, le gain diminue de 20\,\, dB par décade. Il est égal à 1 pour une fréquence f_T dont la valeur correspond au produit GB. Pour certains amplificateurs opérationnels le comportement en fréquence peut être amélioré en ajoutant des composants externes. Une grandeur à prendre également en compte est le temps de montée (Slew rate en anglais) qui caractérise la rapidité de la réponse en sortie à une variation brutale de la tension d'entrée. Il s'exprime en V/\mus.
Le modèle de l'amplificateur idéal est satisfaisant tant que la valeur du gain en boucle ouverte reste très supérieur à celui de la boucle de rétroaction, c'est-à-dire aux basses fréquences. Quand cette condition n'est plus réalisée, il faut reprendre l'étude du circuit en utilisant la valeur du gain donnée par la relation (3).
Nous allons examiner diverses possibilités d'utilisation des amplificateurs opérationnels en utilisant le modèle idéal. Pour déterminer la fonction de transfert, on peut utiliser la relation générale (1) mais le calcul direct est souvent plus rapide.