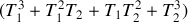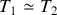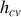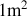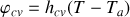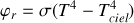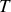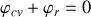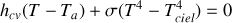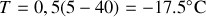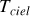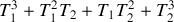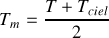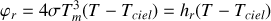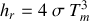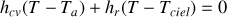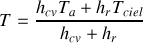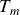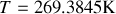Modes de transfert thermique - Température nocturne

Modes de transfert thermique

Température nocturne

Énoncé

On étudie la température nocturne d'une plaque mince posée au sol, que l'on peut considérer comme isolée. Le ciel est très dégagé, et on peut considérer que l'atmosphère - très sèche - est radiativement transparente.

On donne les températures 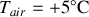, et une température effective 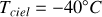.On admet un coefficient d'échange convectif 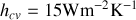. On considère que la plaque a les propriétés d'un corps noir.

Rappeler l'expression des flux d'échange convectif et radiatif de la plaque.
Ecrire le bilan thermique de la plaque en régime permanent établi.
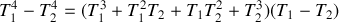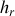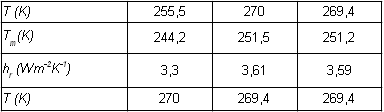
En utilisant l'identité , obtenir une linéarisation du flux radiatif en fonction de la température, et identifier un coefficient d'échange radiatif . En déduire une expression simple pour la température de surface de la plaque.
Calculer à partir d'une technique itérative la température de la plaque. On considérera pour initier le calcul que la température de la plaque est égale à la moyenne des températures de l'air et et du ciel. Conclure.

Aide simple

Solution détaillée

La plaque échange de l'énergie convective avec l'air qui l'entoure, caractérisée par un coefficient d'échange convectif . Le flux convectif pour de surface s'écrit :

L'atmosphére étant radiativement transparente, on peut considérer que la plaque échange radiativement avec le fond du ciel. Le ciel et la plaque étant considérés comme des corps noirs, le flux radiatif pour de surface s'écrit (Loi de Stefan) :

La plaque étant mince, on confondra sa température et sa température de surface .
En régime permanent établi, la plaque est en équilibre thermique avec son environnement. Sa température est le résultat d'un bilan énergétique nul entre les échanges convectif et radiatif :

d'où :
La résolution de l'équation du bilan thermique de la plaque n'est pas triviale. Si, en première approximation, on considère que la température de surface de la plaque est la moyenne des températures du ciel et de l'air, alors . Avec cette approximation, et ne sont pas très éloignées et, dans l'identité donnée dans l'énoncé, chaque terme de la somme peut être approximé par la température moyenne . Alors, il est possible de linéariser le flux radiatif en écrivant
avec défini comme un coefficient d'échange radiatif. L'expression du bilan énergétique se simplifie:

On en déduit :

La température de la plaque s'écrit comme une moyenne pondérée des températures du ciel et de l'air.
La technique itérative est la suivante :
- étant donnée une température de surface de plaque
- on calcule la température moyenne ,
- ce qui permet de calculer le coefficient d'échange
- étant estimé, la dernière équation obtenue fournit la température
- ensuite, on peut à nouveau itérer.
On obtient les résultats consignés dans le tableau suivant :

Tableau 1

Trois itérations suffisent donc à faire converger la solution. A noter que la résolution non approximée de l'équation issue du bilan thermique donne . La linéarisation utilisée donne donc un résultat très satisfaisant.

En conclusion, on obtient une température de surface de plaque qui est négative.

Il peut donc geler dans les déserts.