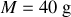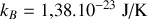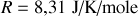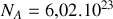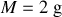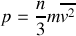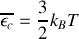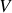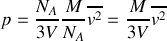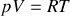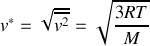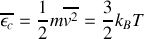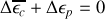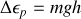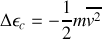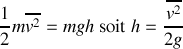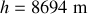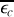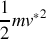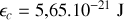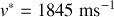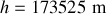1. La vitesse quadratique moyenne des molécules d'un gaz est reliée à la pression de celui-ci :
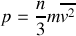
Si l'on considère une mole d'argon et
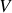 le volume occupé par cette mole. la pression s'écrit
le volume occupé par cette mole. la pression s'écrit
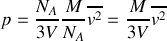
Par ailleurs, le comportement de l'argon est proche de celui d'un gaz parfait. On peut intégrer cette dernière information de deux manières: soit utiliser la loi des gaz parfaits qui relie pression, volume et température du gaz; soit évoquer le principe d'équipartition de l'énergie. Dans le premier cas, on écrit
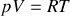 , et par identification avec la relation obtenue plus haut, on obtient :
, et par identification avec la relation obtenue plus haut, on obtient :
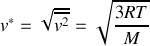
Dans le deuxième cas, on écrit que l'énergie cinétique moyenne de translation des molécules n'est reliée qu'à la température du gaz selon la relation
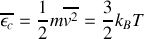 . Et l'on retrouve facilement la même relation.
. Et l'on retrouve facilement la même relation.
Pour les températures demandées, on obtient les valeurs numériques suivantes :
2. A la hauteur verticale maximale atteinte h par la molécule d'argon, l'énergie cinétique de la molécule au niveau du sol a été complètement échangée en énergie potentielle gravitationnelle
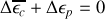
En négligeant les variations de l'accélération de la pesanteur g avec l'altitude,
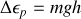 , et par ailleurs
, et par ailleurs
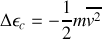 . On en déduit
. On en déduit
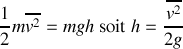
L'application numérique donne
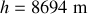 .
.
3. L'énergie cinétique moyenne de translation d'une molécule
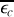 vaut
vaut
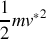 .
.
On obtient à
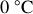
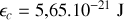
4. Pour une molécule d'hydrogène, on obtient une vitesse
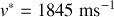 et une hauteur
et une hauteur
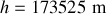 . L'énergie cinétique moyenne de l'hydrogène est bien sûr la même que pour l'Argon à
. L'énergie cinétique moyenne de l'hydrogène est bien sûr la même que pour l'Argon à
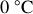 , car elle ne dépend que de la température.
, car elle ne dépend que de la température.
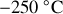 ,
,
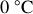 et
et
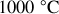 .
.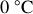 ?
?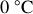 .
.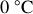 .
.