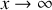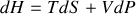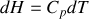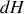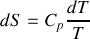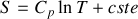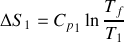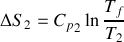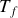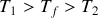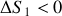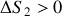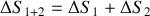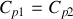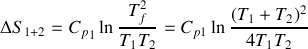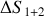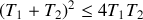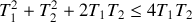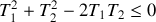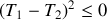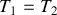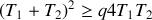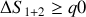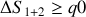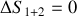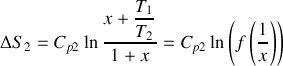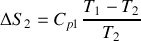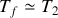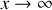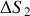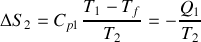Énoncé
Deux corps incompressibles (V =cste), notés 1 et 2, ont pour capacités calorifiques à pression constante
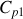 et
et
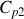 . Initialement isolés aux températures respective
. Initialement isolés aux températures respective
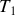 et
et
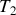 ces deux corps ont été mis en contact thermique sans échange de chaleur avec l'extérieur et à pression constante. Il s'est établi un équilibre thermique et une température finale commune
ces deux corps ont été mis en contact thermique sans échange de chaleur avec l'extérieur et à pression constante. Il s'est établi un équilibre thermique et une température finale commune
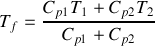 .
.
Calculer les variations d'entropie
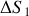 et
et
 de chacun des deux systèmes. Quels sont les signes de
de chacun des deux systèmes. Quels sont les signes de
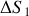 et
et
 (on supposera
(on supposera
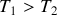 ) ?
) ?On se limite au cas
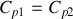 . D´eterminer le signe de la variation d'entropie totale
. D´eterminer le signe de la variation d'entropie totale
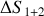 du syst`eme constitu´e des deux corps (1) et (2).
du syst`eme constitu´e des deux corps (1) et (2).Parmi les trois résultats concernant les signes de
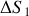 ,
,
 ,
,
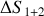 , lesquels pouvaient être prévu à partir d'un principe de la thermodynamique ? Lesquels vous semblent plausible compte-tenu de votre compréhension qualitative de l'entropie ?
, lesquels pouvaient être prévu à partir d'un principe de la thermodynamique ? Lesquels vous semblent plausible compte-tenu de votre compréhension qualitative de l'entropie ?On suppose maintenant que
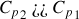 . En notant
. En notant
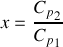 , on se place donc dans la limite où
, on se place donc dans la limite où
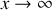 , c'est à dire que le corps (2) a une capacité calorifique “infinie”. Il peut être considéré comme un thermostat vis-à-vis de (1). Calculer alors la variation d'entropie
, c'est à dire que le corps (2) a une capacité calorifique “infinie”. Il peut être considéré comme un thermostat vis-à-vis de (1). Calculer alors la variation d'entropie
 .
.