Dans cette partie, on se place dans le cadre de la mécanique newtonienne. Le référentiel terrestre est supposé galiléen. Dans toutes les expériences étudiées, la température est supposée constante.
Question 1
Quelles réponses donneriez-vous aux questions suivantes posées par un élève de terminale?
a
Qu'appelle-t-on référentiel galiléen?
b
Qu'appelle-t-on mécanique newtonienne?
c
Qu'appelle-t-on fluide parfait?
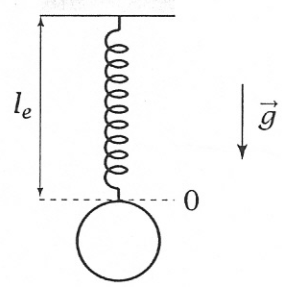
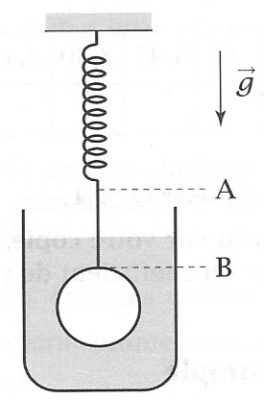
On se propose de déterminer la valeur du coefficient de viscosité
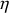d'un liquide. On étudie pour cela le mouvement oscillatoire amorti d'une bille accrochée à un ressort (figure 1). On choisit un axe
dont l'origine est l'extrémité basse du ressort dans la position d'équilibre du système. La direction est la verticale orientée dans le sens descendant.
Question 2
On réalise d'abord l'expérience dans l'air. On utilise une bille sphérique d'aluminium de masse volumique
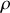, de rayon
cm et de masse
. On accroche la bille à un ressort, supposé sans masse, de raideur
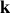et de longueur à vide
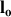. Les notations seront celles de la figure 1.
À l'équilibre du système, la longueur du ressort est
.
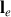a
Établir l'expression de l'allongement du ressort à l'équilibre en fonction des paramètres caractérisant le système.
Calculer sa valeur avec les données suivantes:
Masse volumique de l'aluminium:
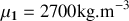; raideur
;
.
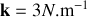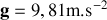b
On écarte, verticalement, la bille de sa position d'équilibre
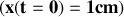et on la lâche sans vitesse initiale
.
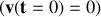En utilisant une approche énergétique, établir l'équation différentielle du mouvement.
En déduire l'expression de la pulsation
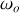et de la période
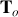des oscillations.
À partir des données numériques précédentes, calculer la valeur de la période
.
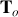Écrire l'équation horaire
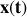du mouvement observé.
c
On appelle «trajectoire de phase» la courbe décrite par un point
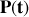de coordonnées
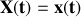et
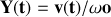dans le plan de phase
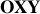. Représenter cette trajectoire de phase.
La forme de cette courbe permet-elle de déterminer la nature du mouvement?
Question 3
On effectue maintenant l'expérience en plongeant la bille dans de l'huile de viscosité
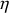que l'on cherche à déterminer. La masse volumique de cette huile est égale à :
.
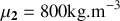Les notations sont celles de la figure 2.
La tige
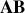est supposée de masse nulle, le frottement de l'huile et la poussée d'Archimède sur cette tige sont supposés nuls. Le ressort n'entre pas dans l'huile.
a
L'allongement du ressort dans sa position d'équilibre est-il identique à celui de la question 2.a) ? Justifier la réponse.
b
On suppose que, dans l'huile, la sphère est soumise à une force de frottement donnée par la loi de Stockes :
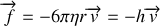
Le coefficient de viscosité
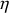se mesure en poiseuille (PI). Quelle est la dimension de cette grandeur ?
c
On écarte à nouveau la sphère de sa position d'équilibre d'une longueur
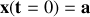et on la lâche sans vitesse initiale. Établir l'équation différentielle du mouvement.
d
On pose
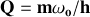. Établir l'expression de
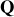en fonction de
et
.
e
Lorsque
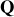> 1, donner l'expression de la pseudo-période
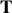du mouvement ainsi que la forme générale de
.
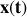On appelle «décrément logarithmique» la grandeur
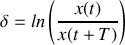. Établir son expression en fonction de
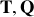et
.
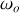À des intervalles de temps successifs et égaux à une pseudo-période, on mesure les élongations maximales du ressort. Les valeurs expérimentales obtenues sont reportées dans le tableau suivant:
Ces valeurs permettent de supposer
.
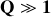Après avoir complété le tableau sur votre copie, déduire de cette expérience les valeurs du coefficient
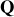et du coefficient de viscosité
.
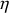