On considère le mouvement d'un pendule simple qui oscille dans un milieu où les forces de frottement sont inexistantes. Le pendule est constitué d'un objet ponctuel
de masse
, accroché par l'intermédiaire d'un fil rigide à un point fixe
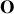(figure 3).
On suppose le fil rigide sans masse. Sa longueur est
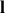= 1 m. On note
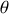l'angle du fil
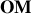avec la verticale. Son orientation est précisée sur la figure 3. L'ensemble est situé dans le champ de pesanteur terrestre, considéré comme uniforme. On écarte le pendule de sa position d'équilibre d'un angle
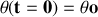et on le lâche sans vitesse initiale.
Question 1 : Oscillations de faible amplitude
a
Énoncer le théorème du moment cinétique appliqué à un point matériel.
b
Montrer que la trajectoire du point matériel
est plane.
c
Établir l'équation différentielle vérifiée par l'angle
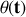en fonction du temps.
Donner l'expression de la pulsation
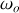du mouvement.
d
20 périodes correspondent à une durée de 40,12 s. En déduire une valeur de
.
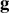Question 2 : Cas général
On se place maintenant dans le cas d'oscillations d'amplitude plus importante. On désigne par
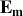l'énergie mécanique, par
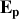l'énergie potentielle et par
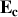l'énergie cinétique du pendule.
a
Donner les expressions des énergies cinétique et potentielle en fonction de
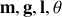et
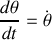(On prendra comme origine pour l'énergie potentielle
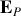= 0 pour
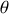= 0)
b
En déduire que l'équation de la trajectoire dans le plan de phase du point
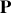de coordonnées
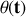et
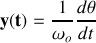peut se mettre sous la forme:
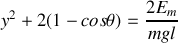
c
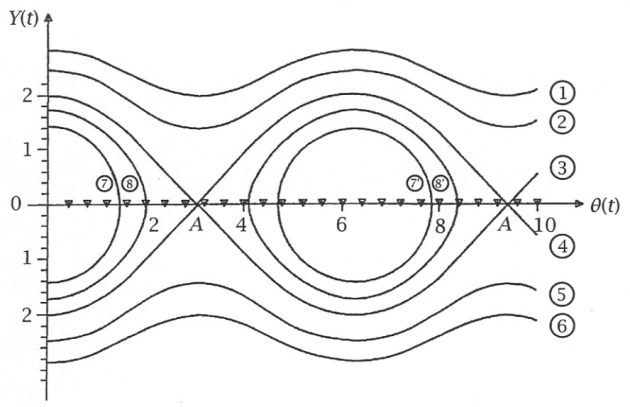
L'allure générale du portrait de phase de cette équation est donnée à la figure 4. En reprenant les notations de cette figure:
Quelles sont les trajectoires de phase correspondant à
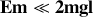? À quelle situation correspondent les points
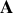de la figure 4 ?Quelles sont les courbes correspondantes:
i. À un mouvement oscillatoire périodique autour d'une position d'équilibre stable?
ii. À un mouvement de révolution?
