Réponse 1
a
Un référentiel galiléen est un référentiel dans lequel est vérifié le principe de l'inertie (ou première loi de Newton): un point matériel soumis à aucune interaction extérieure, est au repos ou a un mouvement rectiligne et uniforme.
b
Dans le cadre de la mécanique Newtonienne, les trois lois suivantes peuvent s'appliquer:
principe de l'inertie (définition d'un référentiel galiléen);
principe fondamental de la dynamique (ou deuxième loi de Newton);
principe des actions réciproques.
La mécanique Newtonienne ne comprend donc pas la mécanique relativiste, puisque le principe d'action et de la réaction n'est pas général en relativité (rappelons que ce principe est lié à une propagation instantanée des interactions).
c
Dans le cas du gaz parfait monoatomique, les atomes sont supposés identiques ponctuels (i.e. on néglige leur diamètre devant la distance moyenne qui les sépare), rigides; toutes les collisions sont supposées conserver l'énergie (on parle de « collisions élastiques »). Enfin, les vecteurs positions
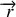 et vitesses
et vitesses
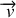 des atomes sont supposés distribués au hasard (on parle de «chaos »). Dans un fluide (comme un liquide), comme pour le «gaz » parfait, un élément de volume du fluide ne subit que des actions normales à ses surfaces (la viscosité est donc nulle).
des atomes sont supposés distribués au hasard (on parle de «chaos »). Dans un fluide (comme un liquide), comme pour le «gaz » parfait, un élément de volume du fluide ne subit que des actions normales à ses surfaces (la viscosité est donc nulle).
Réponse 2
a
Allongement du ressort à l'équilibre :
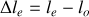
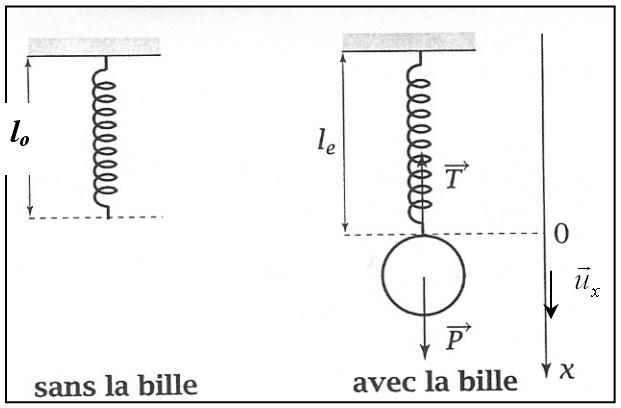
Référentiel : terrestre supposé galiléen
Système : bille de masse
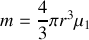
Bilan des forces :
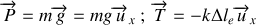
À l'équilibre : on a
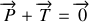 (principe fondamental de la dynamique), soit en projetant selon
(principe fondamental de la dynamique), soit en projetant selon
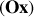 :
:
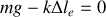 .
.
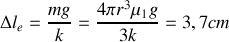
b
Le poids et la tension sont des forces conservatives ; Le système est donc conservatif et l'énergie mécanique se conserve :
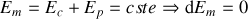 .
.
L'abscisse
 repère la masse
repère la masse
 par rapport à sa position d'équilibre
par rapport à sa position d'équilibre
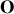 .
.
À un instant
 la résultante des forces est :
la résultante des forces est :
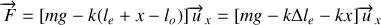 .
.
Avec la condition d'équilibre on a
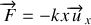 qui dérive de l'énergie potentielle
qui dérive de l'énergie potentielle
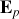
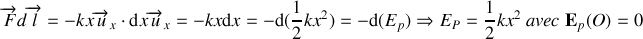 .
.
L'énergie cinétique :
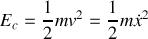 et l'énergie mécanique :
et l'énergie mécanique :
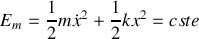 .
.
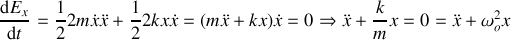 (équation différentielle de l'oscillateur harmonique).
(équation différentielle de l'oscillateur harmonique).
On a donc
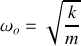 (pulsation des oscillations)et la période des oscillations
(pulsation des oscillations)et la période des oscillations
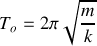 .
.
Application numérique
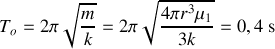
Équation horaire
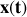 du mouvement :
du mouvement :
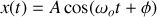
Conditions initiales
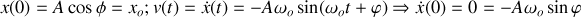
Les solutions sont
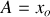 et
et
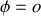 et donc
et donc
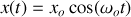 :
:
c
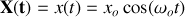
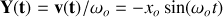
On a
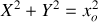 et donc
et donc
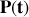 décrit un cercle de rayon
décrit un cercle de rayon
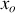 dans le sens inverse du sens trigonométrique.
dans le sens inverse du sens trigonométrique.
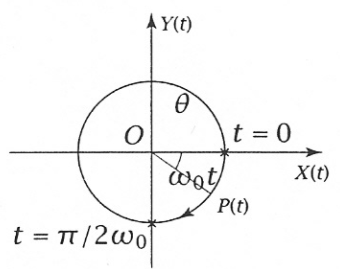
La nature circulaire de la courbe atteste du caractère harmonique (ou quasi-sinusoïdal) des oscillations.
De plus,
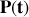 décrit une courbe fermée caractéristique d'un mouvement périodique.
décrit une courbe fermée caractéristique d'un mouvement périodique.
Réponse 3
a
L'allongement à l'équilibre du ressort est différent, puisque la bille est soumise, en plus de son poids et de la force de rappel du ressort, à la poussée d'Archimède de l'huile. On peut d'avance affirmer que le ressort sera moins étiré.
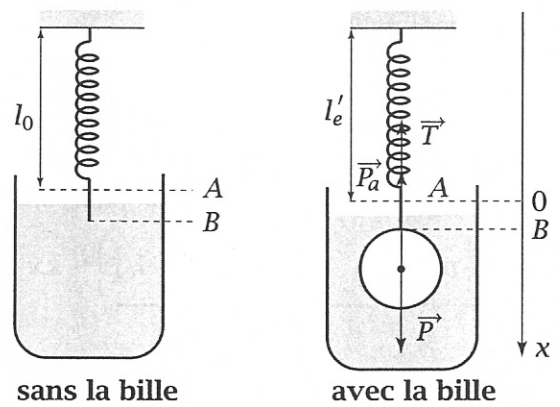
Bilan des forces s'exerçant sur la bille:
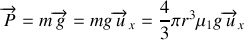
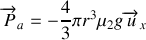 (poussée d'Archimède)
(poussée d'Archimède)
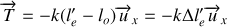
À l'équilibre :
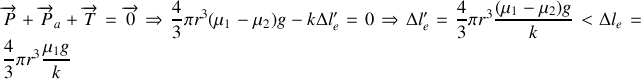
b
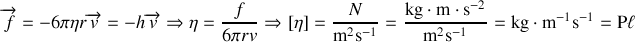
Remarque :
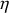 est homogène à une pression x temps et parfois exprimée en Pa.s.
est homogène à une pression x temps et parfois exprimée en Pa.s.
c
Appliquons le principe fondamental de la dynamique à la bille dans le référentiel terrestre supposé galiléen :
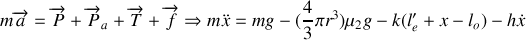
Avec :
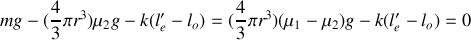 (condition d'équilibre),
(condition d'équilibre),
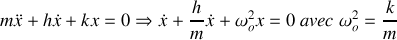
la pulsation propre de l'oscillateur
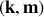 .
.
d
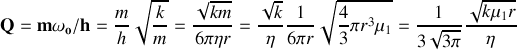
Avec
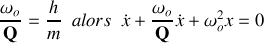
e
Le discriminant
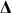 de l'équation caractéristique
de l'équation caractéristique
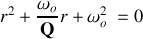 associée à l'équation différentielle du mouvement vaut :
associée à l'équation différentielle du mouvement vaut :
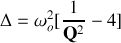 . On distingue 3 cas selon la valeur de
. On distingue 3 cas selon la valeur de
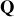 :
:
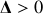
 Q< ½ régime apériodique
Q< ½ régime apériodique
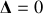
 Q = ½ régime critique
Q = ½ régime critique
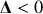
 Q> ½ régime pseudo-périodique
Q> ½ régime pseudo-périodique
Pour
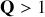 , le régime est pseudo-périodique et les solutions de l'équation caractéristiques sont :
, le régime est pseudo-périodique et les solutions de l'équation caractéristiques sont :
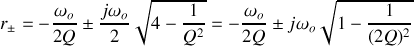
Les solutions de l'équation différentielle du mouvement sont de la forme :
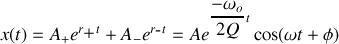
avec
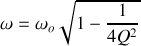
La pseudo-période
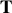 du mouvement
du mouvement
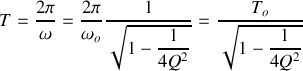
Le « décrément logarithmique »
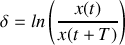 traduit l'amortissement de l'amplitude des oscillations sur une période. On a :
traduit l'amortissement de l'amplitude des oscillations sur une période. On a :
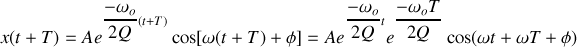
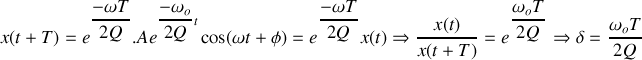
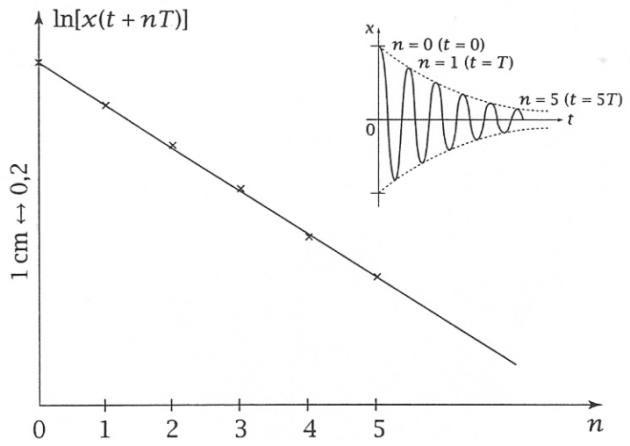
À des intervalles de temps successifs et égaux à une pseudo-période, on mesure les élongations maximales du ressort. Les valeurs expérimentales obtenues sont reportées dans le tableau suivant:
On a
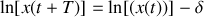
En choisissant la première valeur de x comme origine des oscillations (n =0), au bout de n périodes on a :
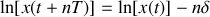
Si on trace
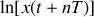 en fonction de n on peut espérer obtenir une droite de pente
en fonction de n on peut espérer obtenir une droite de pente
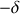 .
.

On obtient
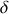 = 0,3 et
= 0,3 et
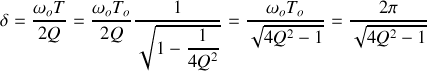
Soit :
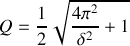
Application numérique
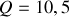 et
et
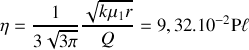 .
.