Réponse 1 : Oscillations de faible amplitude
a
Dans un référentiel galiléen, la dérivée par rapport au temps du moment cinétique du point matériel évalué en un point
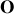 est égale à la somme des moments des forces qui lui sont appliquées en
est égale à la somme des moments des forces qui lui sont appliquées en
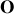 , à condition que ce dernier soit fixe.
, à condition que ce dernier soit fixe.
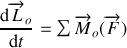 (O point fixe dans le référentiel d'étude)
(O point fixe dans le référentiel d'étude)
b
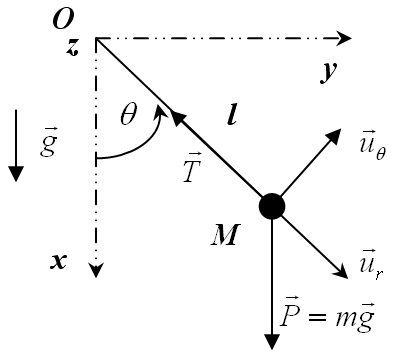
On se place dans le référentiel terrestre supposé galiléen et l'on considère le point matériel
 . Les forces qui lui sont appliquées sont son poids
. Les forces qui lui sont appliquées sont son poids
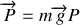 et la tension
et la tension
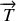 du fil auquel il est accroché.
du fil auquel il est accroché.
Si l'on applique la relation fondamentale de la dynamique à
 , on a :
, on a :
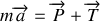
Projetée selon
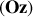 , cette relation donne:
, cette relation donne:
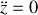 d'où, en intégrant,
d'où, en intégrant,
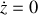 (puisque
(puisque
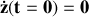 ) et donc
) et donc
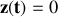 pour tout
pour tout
 car
car
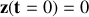 .
.
En conséquence, le mouvement du pendule a lieu dans le plan
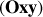 .
.
c
Notons
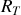 le référentiel terrestre supposé galiléen. On applique le théorème du moment cinétique au point matériel
le référentiel terrestre supposé galiléen. On applique le théorème du moment cinétique au point matériel
 en
en
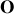 fixe:
fixe:
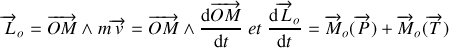
D'après la symétrie du problème, un passage en coordonnées polaires paraît judicieux.
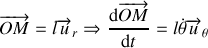
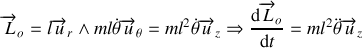
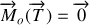 (ligne d'action passe par
(ligne d'action passe par
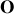 )
)
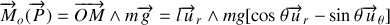
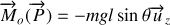
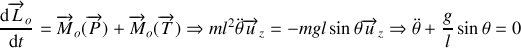
Oscillations de faibles amplitudes
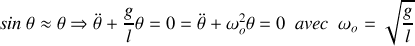 avec On obtient l'équation du mouvement d'un oscillateur harmonique de pulsation
avec On obtient l'équation du mouvement d'un oscillateur harmonique de pulsation
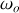 .
.
d
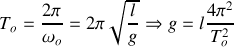
Application numérique
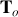 = 40,12/20=2,006 s. ce qui donne
= 40,12/20=2,006 s. ce qui donne
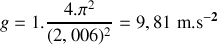
Remarque :
l étant donnée avec un seul chiffre significatif, malgré la précision de mesure de To, on devrait donner pour résultat
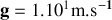
Réponse 2 : Cas général
a
L'énergie cinétique :
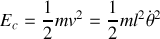
Énergie potentielle:
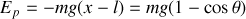 (signe - car l'axe des x est orienté vers le bas) avec la convention d'origine
(signe - car l'axe des x est orienté vers le bas) avec la convention d'origine
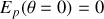 (la force de tension ne travaille pas donc seule l'énergie potentielle de pesanteur intervient).
(la force de tension ne travaille pas donc seule l'énergie potentielle de pesanteur intervient).
b
L'énergie mécanique du pendule
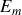 est la somme de son énergie cinétique et de son énergie potentielle :
est la somme de son énergie cinétique et de son énergie potentielle :
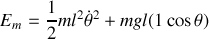 Si l'on néglige les forces des frottements, le pendule n'est soumis à aucune force non conservatrice et son énergie mécanique se conserve. Soit le point
Si l'on néglige les forces des frottements, le pendule n'est soumis à aucune force non conservatrice et son énergie mécanique se conserve. Soit le point
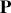 de coordonnées
de coordonnées
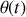 et
et
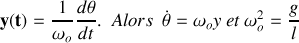 :
:
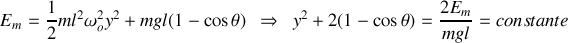
c
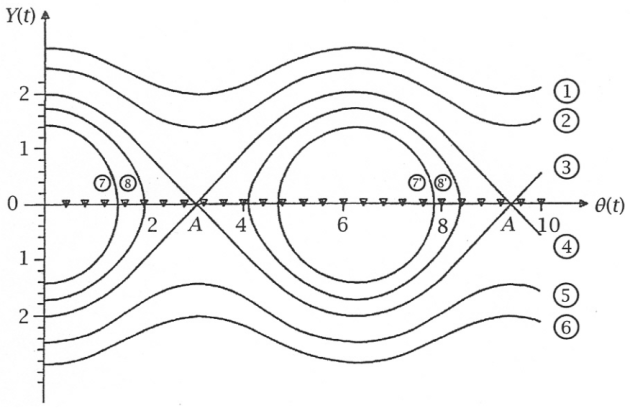
Trajectoires de phase : cas
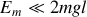 : pour que le pendule fasse un tour complet, il faut qu'il puisse atteindre la position
: pour que le pendule fasse un tour complet, il faut qu'il puisse atteindre la position
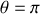 avec au minimum
avec au minimum
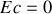 , soit
, soit
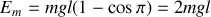 .
.
Si
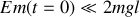 , alors le mouvement du pendule ne sera pas révolutif mais oscillatoire et périodique: cela correspond aux courbes 7-8 et 7'-8'.
, alors le mouvement du pendule ne sera pas révolutif mais oscillatoire et périodique: cela correspond aux courbes 7-8 et 7'-8'.
Les points
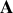 correspondent aux points
correspondent aux points
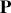 pour lesquels
pour lesquels
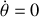 et
et
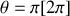 . Ces points sont caractérisés par un changement de signe de
. Ces points sont caractérisés par un changement de signe de
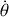 , et donc par un demi-tour du pendule:
, et donc par un demi-tour du pendule:

On est dans le cas où
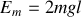 . Ce sont les trajectoires 3 et 4
. Ce sont les trajectoires 3 et 4
Quelles sont les courbes correspondantes ?
i. Les positions d'équilibre stables du pendule correspondent à
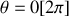 . De plus, une trajectoire périodique se caractérise par une courbe fermée dans le plan de phase.
. De plus, une trajectoire périodique se caractérise par une courbe fermée dans le plan de phase.
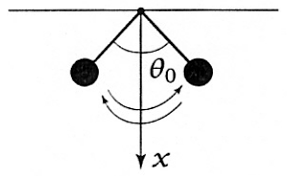
D'après ces considérations, les courbes 7 et 8 correspondent à un mouvement oscillatoire périodique autour de la position stable
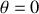 . Les courbes 7' et 8' sont, elles, représentatives d'un mouvement oscillatoire périodique autour de la position stable
. Les courbes 7' et 8' sont, elles, représentatives d'un mouvement oscillatoire périodique autour de la position stable
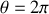 (identique à
(identique à
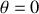 ).
).
À noter que la courbe 7 (ou 7'), circulaire, traduit le caractère harmonique (ou quasi-sinusoïdal) des oscillations.
En revanche, la courbe 8 (ou 8') est relative à un mouvement d'amplitude
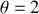 rad, soit
rad, soit
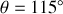 , et le fait qu'elle soit non circulaire est dû au caractère non sinusoïdal des oscillations de forte amplitude.
, et le fait qu'elle soit non circulaire est dû au caractère non sinusoïdal des oscillations de forte amplitude.
ii. Au cours d'un mouvement de révolution, le pendule tourne toujours dans le même sens, et donc sa vitesse garde un signe constant, tout en étant maximale pour
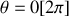 et minimale pour
et minimale pour
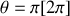 : ces caractéristiques sont celles des courbes 1 et 2 pour lesquelles
: ces caractéristiques sont celles des courbes 1 et 2 pour lesquelles
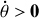 et des courbes 5 et 6 pour lesquelles
et des courbes 5 et 6 pour lesquelles
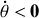 .
.