Un dipôle \mathbf {(AB)} est constitué d'un conducteur ohmique de résistance \mathbf R, d'une bobine d'inductance \mathbf L, de résistance négligeable et d'un condensateur de capacité \mathbf C branchés en série.
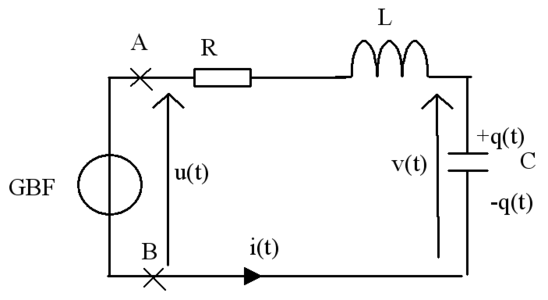
Il est alimenté par un générateur basse fréquence, supposé idéal, qui délivre une tension alternative sinusoïdale \mathbf {u(t)} de valeur efficace \mathbf U_o : u(t) = U_o \sqrt 2 \cos \omega t (\mathbf \omega est la pulsation et \mathbf t le temps).
Question 1 : Étude de la tension v(t) aux bornes du condensateur de capacité C
En tenant compte des conventions indiquées sur le schéma, écrire les relations entre v(t) et q(t), et entre i(t) et q(t).
On pose \omega_o = \frac{1}{\sqrt{L C}} et Q_o = \frac{\sqrt L}{ R \sqrt C}.
Calculer la valeur de ces grandeurs pour: \mathbf R = 135 \Omega, \mathbf L = 0,04 H et \mathbf C = 22 ~nF.
Écrire l'équation différentielle vérifiée par la tension v(t) aux bornes du condensateur en faisant apparaître la tension u(t) et les grandeurs \omega _o et Q_o.
Question 2. Étude du régime forcé
Pourquoi dit-on que le dipôle \mathbf {(AB)} est en régime forcé ? Quelle est l'allure de la courbe observée lorsqu'on applique la tension \mathbf {v(t)} aux bornes d'un oscilloscope utilisé en mode balayage ?
On note \underline {u(t)} et \underline {v(t)} les tensions complexes associées aux tensions \mathbf {u(t)} et \mathbf {v(t)}. Établir l'expression de la fonction de transfert H(j \omega ) = \frac{\underline {v(t)}}{\underline {u(t)}} en fonction de x= \frac{\omega}{\omega_o}.
Le générateur délivrant une tension de pulsation \mathbf \omega = 31 500 ~ rad.s^{-1}, on observe simultanément les variations de \mathbf {u(t)} et de \mathbf {v(t)} sur l'écran d'un oscilloscope utilisé en mode balayage. La tension \mathbf {v(t)} aux bornes du condensateur est-elle en « avance ou en retard de phase sur la tension \mathbf {u(t)} délivrée par le générateur? Calculer le déphasage \mathbf \varphi entre \mathbf {u(t)} et \mathbf {v(t)}.
Question 3. Étude la résonance en intensité
Donner l'expression de l'impédance complexe \underline Z du dipôle \mathbf {(AB)} en fonction de la résistance \mathbf R du dipôle \mathbf {(AB)}, de \mathbf Q_o et de \mathbf x. Pour une tension de pulsation \mathbf \omega = 31 500 rad.s^-1, calculer la valeur de l'impédance réelle \mathbf Z du circuit avec les données numériques de la question \mathbf {1.b}.
En déduire qu'il existe un maximum d'intensité dans le dipôle \mathbf {(AB)} lorsque la pulsation \mathbf \omega du générateur varie.
Pour \mathbf {U_o} = 5,4 volts , calculer, à la résonance, les valeurs de l'intensité efficace \mathbf I_o dans le circuit et de la tension efficace \mathbf V_o aux bornes du condensateur.
Qu'appelle-t-on «bande passante» à moins trois décibels du dipôle \mathbf {(AB)} pour la résonance en intensité ? Établir l' expression de la largeur \mathbf {\Delta \omega} de cette bande passante en fonction de \omega_o et Q_0. Calculer \mathbf {\Delta \omega} . Que caractérise le coefficient \mathbf Q_0 ?