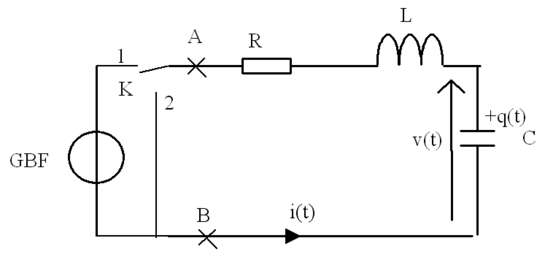
Le dipôle \mathbf {(AB)} précédent est maintenant relié à un commutateur à deux voies \mathbf K. (fig. 2). Lorsque le commutateur \mathbf K est basculé en position 1, le condensateur se charge sous la tension \mathbf E délivrée par un générateur de tension constante. Le condensateur une fois chargé, on bascule à \mathbf t=0 le commutateur \mathbf K en position 2.
Question 1
Quelle est l'équation différentielle vérifiée par la tension \mathbf {v(t)} aux bornes du condensateur pour des instants t \geq 0 ?
Question 2
Quelles sont les conditions initiales de la décharge du condensateur: tension \mathbf {v(t} = 0) et courant initial \mathbf {i(t} = 0) ?
Question 3
Afin d'obtenir une forme réduite de l'équation différentielle, on introduit la grandeur \tau = \frac{t}{\sqrt {LC}} et le degré d'amortissement \alpha = \frac{R}{2} \sqrt \frac{C}{L}.
Écrire l'équation différentielle réduite vérifiée par la tension \mathbf {v(\tau)} aux bornes du condensateur, en introduisant les variables \mathbf \tau et \mathbf \alpha .
Question 4
Montrer, sans résoudre l'équation différentielle, qu'il existe, selon les valeurs de l'amortissement \mathbf \alpha , deux régimes principaux d'évolution de la tension \mathbf{v(\tau)} . Donner l'allure des variations de la tension \mathbf{v(\tau)} dans chacun de ces deux régimes.
Question 5
Pour quelle valeur de \mathbf \alpha passe-t-on d'un régime à l'autre ? Pour cette valeur de \mathbf \alpha , donner l'expression de la résistance du circuit. Comment nomme-t-on cette résistance ? Calculer sa valeur pour le circuit précédent avec \mathbf L = 0,04 H et \mathbf C = 22 nF.