v(t) = \frac{q(t)}{C} ~~et~~ i(t) = - \frac{d q(t)}{dt}

\omega_o = \frac{1}{\sqrt{LC}} = \frac{1}{\sqrt{4.10^{-2}.22.10^{-9}}} = 33,7.10^3 rad.s^{-1}

Q_o = \frac{ \sqrt L }{R \sqrt C } = \frac{\sqrt{4.10^{-2}}}{135 \sqrt{22.10^{-9}}} = 10 .

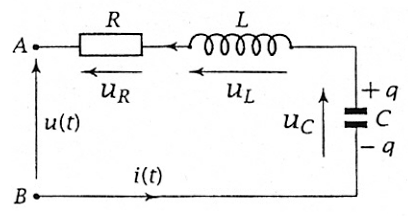
Loi des mailles : u(t) = u_R + u_L + u_C

u(t) = - Ri(t) - L \frac{di}{dt} + v(t) ~~avec~~ i(t) = - \frac{dq(t)}{dt} = - C \frac{dv}{dt} \Rightarrow u(t) = RC \frac{dv}{dt} + LC \frac{d^2 v}{dt^2} + v(t)

\frac{d^2 v}{d t^2} + \frac{R}{L} \frac{dv}{dt} + \frac{1}{LC} v(t) = \frac{1}{LC} u(t)

et avec \omega _o ^2 = \frac{1}{LC} et \frac{\omega_o}{\mathbf Q_o} = \frac{R}{L} on obtient :

\frac{d^2 v}{dt^2} + \frac{\omega_o}{Q_o} \frac{dv}{dt} + \omega_o^2 v(t) = \omega_o^2 u(t)

Le dipôle \mathbf {(AB)} est en régime forcé car on impose une tension extérieure, sinusoïdale de pulsation \mathbf \omega, \mathbf {u(t)} à ses bornes.

Si on applique \mathbf {v(t)} aux bornes d'un oscilloscope utilisé en mode balayage, on observe une variation sinusoïdale de Français : \mathbf {v(t)} de même pulsation \mathbf \omega .

. Notation complexe : \underline {u(t)} = \underline u e^{j \omega t} = u e^{j \omega t} et \underline {v(t)} = \underline v e^{j \omega t} = v e^{j \varphi} e^{j \omega t}.

On a : \frac{d \underline v}{d t} = j \omega \underline v e^{j \omega t} et \frac{d^2 \underline v}{d t^2} = - \omega^2 \underline v e^{j \omega t} . En simplifiant par e^{j \omega t} , l'équation différentielle devient :

- \omega^2 \underline v + \frac{\omega_o}{Q_o}(j \omega) \underline v + \omega_o^2 \underline v = \omega^2_o \underline u ~~\Rightarrow ~~ [\omega_o^2 - \omega^2 + j \frac{\omega \omega_o}{Q_o}]\underline v = \omega_o^2 \underline u ~~\Rightarrow

H(j \omega ) = \frac{\underline{v(t)}}{\underline {u(t)}} = \frac{\underline v}{ \underline u} = \frac{1}{1 - \frac{\omega^2}{\omega_o^2} +\frac{j}{Q_o} \frac{\omega}{\omega_o}} = \frac{1}{1 - x^2 + \frac{j}{Q_o}x}

avec x = \frac{\omega}{\omega_o}

On impose \mathbf {\omega = 31 500 ~rad.s-1< \omega_o = 33 700 ~rad.s-1  ~donc~ \mathbf x < 1}. On a :

\vert \underline v \vert = \frac{ u }{ \sqrt { (1-x^2) ^2 + \frac{x^2}{Q_o^2}} } = v ~~et~~ arg ( \underline v ) = \varphi = arg( \underline u ) - arg(1 - x^2 + \frac{jx}{Q_o}) = -arg (1 - x^2 + \frac {jx}{Q_o} )

\tan \varphi = - \frac{x}{Q_o(1 - x^2) }

x=\frac{\omega}{\omega_o} = 0,935 et \mathbf Q_o = 10 soit \tan \mathbf \phi= -0,74 ~ et ~ \mathbf \phi = -36,5° \mathbf \rightarrow \mathbf{v(t)} est en retard sur \mathbf {u(t)}.

On a \underline{u_{AB}} = \underline {Z i } ~~et~~ u_{AB} = - R i - L \frac{di}{dt} + \frac{q}{C} = - Ri - L \frac{di}{dt} + \frac{1}{C} \int idt ~~( car ~i(t) ~~ = - \frac{dq}{dt})

\underline {u_{AB}} = [ - R - j L \omega - \frac{1}{j C \omega } ] i ~~ \Rightarrow \underline Z = - [ R + j(L \omega - \frac{1}{C \omega})]

Avec : \omega_o ^2 = \frac{1}{LC} ~, ~on~a~ L = \frac{1}{C \omega_o ^2} ~et~ Q_o ^2 = \frac{L}{R^2 C} = \frac{1}{R^2 C^2 \omega_o ^2} \Rightarrow C = \frac{1}{R \omega_o Q_o } ~et~ L = \frac{R Q_o}{\omega_o}:

\underline Z = - [R + jL \omega - \frac{j}{C \omega} ] = - [ R + jRQ_o x - \frac{jRQ_o}{\omega_o}] \Rightarrow \underline Z = - R [1 + jQ_o (x - \frac{1}{x})]

On a : \vert \underline Z \vert = Z = R \sqrt {{1 + Q_o^2 (x - \frac{1}{x}})^2 }

Z = 135 \sqrt {1 + 100 (0,935 - \frac{1}{0,935})^2 } = 227 \Omega

On a u(t) = U_o \sqrt 2 \cos \omega t et i(t) = I_o \sqrt 2 \cos (\omega t + \phi) .

v(t) = \frac{q}{C} = - \frac{1}{C} \int idt \Rightarrow \underline v = - \frac{1}{jC \omega } \underline i \Rightarrow \phi = Arg \underline i = Arg \underline v - Arg (jC \omega) = \varphi - \frac{\pi}{2}

on a \underline u = - \underline {Z i} \Rightarrow \vert \underline i \vert = I_o \sqrt 2 = \frac{\vert \underline u \vert}{\vert \underline Z \vert} = \frac {U_o \sqrt 2}{Z} : \mathbf {I_o(ω)} est maximale quand \mathbf Z est minimale. Il est évident que \mathbf Z est minimale quand le terme \mathbf {( x - \frac{1}{x})^2} est minimale c'est-à-dire quand il est nul soit : x^2 = 1 \Rightarrow \omega = \omega_o .

Le maximum d'intensité dans le dipôle \mathbf {AB} correspond donc à une pulsation \mathbf \omega du générateur égale à la pulsation propre \mathbf ω_o du circuit \mathbf {(L,C)} : c'est la résonance d'intensité.

Si x^2 =1 \Rightarrow \omega = \omega_o alors Z=R .

I_o = \frac {U_o}{Z} \Rightarrow I_{oR} = \frac{U_o}{R} et pour x = 1 alors \vert \underline H(j \omega_o) \vert = Q_o \Rightarrow V_o = Q_o U_o .

\mathbf Q_o = 10 ~ et~\mathbf Uo = 5,4 \mathbf V, \mathbf I_o = 40 ~\mbox {mA}  ~et ~V_o = 54~\mathbf V d'où l'appellation de facteur de surtension \mathbf Q_o.

La bande passante à moins \mathbf {3~dB} du dipôle \mathbf {AB} pour la résonance en intensité correspond à la bande en fréquence \mathbf {[f_{min} ; f_{max}]} telle que :

I_o (f_{min}) = I_o (f_{max}) = \frac{I_{oR}}{\sqrt 2} et alors

\forall ~f~ \in [f_{min}  ; f_{max}] , ~~ I_o(f) \geq \frac{I_{oR}}{\sqrt 2} = \frac{U_o}{\sqrt 2 R}

\Delta f = f_{max} -f_{min} : bande passante à \mathbf {–3dB}

Sachant que \omega = 2 \pi f , on peut calculer la largeur de la bande passante en évaluant \mathbf {\Delta \omega} en \mathbf {rad.s^{-1}} puis revenir à \Delta f = \frac{\Delta \omega}{2 \pi}

Il faut donc résoudre l'équation :

I_o = \frac{U_o}{Z} = \frac{I_{oR}}{R \sqrt 2} = \frac{U_o}{R \sqrt 2} \Rightarrow Z = R \sqrt 2 \Rightarrow Z^3 = 2 R^2

On a donc : 2 = 1 + Q_o ^2 (x - \frac{1}{x})^2 \Rightarrow x - \frac{1}{x} = \pm \frac{1}{Q_o} \Rightarrow x^2 \pm \frac{1}{Q_o} x - 1 = 0

Le discriminant de cette équation du second degré vaut \Delta = \frac{1}{Q_o^2 }+4 > 0. Pour un signe donné(+ ou -) dans l'équation de départ, on obtient deux solutions réelles de signes opposés (produit des racines = \mathbf{-1<0}). Comme \mathbf x doit être positive (rapport de 2 pulsations) seules les solutions positives sont acceptables.

x^2 + \frac{1}{Q_o}x - 1 = 0 ~~\Rightarrow~~ x_\mbox{+} = - \frac{1}{2 Q_o} + \frac{1}{2 Q_o} \sqrt {1 + 4 Q_o^2}

x^2 + \frac{1}{Q_o}x - 1 = 0 ~~\Rightarrow~~ x_\mbox{+} = + \frac{1}{2 Q_o} + \frac{1}{2 Q_o} \sqrt {1 + 4 Q_o^2}

x = \frac {\omega}{\omega_o} \Rightarrow \Delta \omega = \omega_o \Delta x = \omega_o [x_\mbox{-} - x_\mbox{+}] = \frac{\omega_o}{Q_o} = 3370  rad.s^{-1}

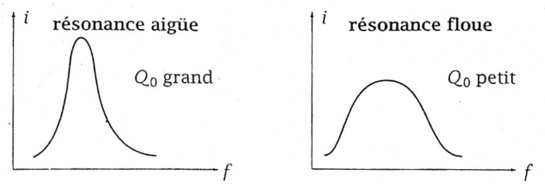
Q_o = \frac{\omega_o}{\Delta \omega} est appelé facteur de qualité et caractérise l'acuité de résonance.

Lorsque \mathbf Q_o est grand, pour \mathbf \omega_o donnée, \Delta \omega est faible : on parle alors de résonance aiguë, le circuit \mathbf {(R, L, C)} est dit sélectif en fréquences, l'amplitude du courant ne prend des valeurs importantes que sur une petite gamme de fréquences.

Lorsque \mathbf Q_o est petit, pour \mathbf \omega_o donnée, \Delta \omega est grand : on parle alors de résonance floue, le circuit \mathbf{(R, L, C)} est alors peu sélectif en fréquences, il ne privilégie pas vraiment de fréquences.