À t \geq 0 , le commutateur \mathbf K est basculé en position 2. Le circuit \mathbf {(R, L, C)} est donc fermé sur lui-même. L'équation différentielle vérifiée par la tension \mathbf {v(t)} aux bornes du condensateur est l'équation vu à la question D.I.1.3. en prenant \mathbf {u(t)} = 0

\frac{d^2 v}{dt^2} + \frac{\omega_o}{Q_o} \frac{dv}{dt} + \omega_o^2 v(t) = 0

avec \omega_o = \frac{1}{\sqrt{LC}} et Q_o = \frac{\sqrt L}{R \sqrt{C}}

À \mathbf {t=0} , le condensateur a été chargé sous la tension +E et donc : v(t=0) = + E et i(t=0) = 0 (il n'y a plus de variation temporelle de la charge).Ensuite, pour t \geq 0 , ces grandeurs évoluent de manière continue puisque la tensions aux bornes d'un condensateur est continue \mathbf {(v)} et le courant dans une bobine également \mathbf {(i)}.

Avec \tau = \frac{t}{\sqrt{LC}} = \omega_o t ~~~~ \frac{d \tau}{dt} = \omega_o

et \frac{dv}{dt} = \frac{dv}{d \tau} \frac{d \tau}{dt} = \omega_o \frac{dv}{d \tau} ~~~~ et ~~~~ \frac{d^2 v}{dt^2} = \frac{d}{d \tau}(\frac{dv}{dt}) \frac{d \tau}{dt} = \omega_o \frac{d^2 v}{d \tau^2} \omega_o = \omega_o^2 \frac{d^2 v}{ d \tau^2}

L'équation différentielle devient \omega_o^2 \frac{d^2 v}{d \tau^2}+\frac{\omega_o^2}{Q_o} \frac{dv}{d \tau}+ \omega_o ^2 v(t)=0 . En simplifiant par \mathbf \omega_o^2 et en utilisant le degré d'amortissement \alpha = \frac{R}{2} \sqrt{\frac{C}{L}}= \frac{1}{2 Q_o} , on obtient :

\frac{d^2v}{d \tau^2} + 2 \alpha \frac{dv}{d \tau} + v(t) = 0

L'équation caractéristique associée à l'équation différentielle précédente est :

r^2 + 2 \alpha r = 1 = 0

Son discriminant vaut \Delta = 4 \alpha^2 - 4 = 4(\alpha^2 -1) . D'après son expression, on sait que \alpha > 0 et donc 2 principaux cas à distinguer :

\alpha >1 alors le discriminant est positif et on obtient 2 solutions réelles négatives pour \mathbf r et une solution amortie exponentiellement non oscillante pour \mathbf {v(t)}.

Amortissement fort, régime apériodique

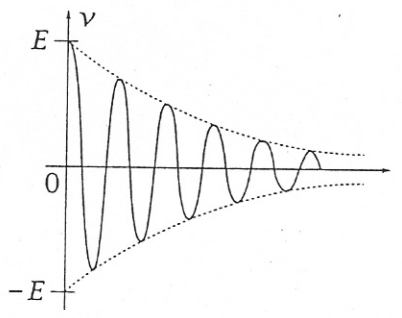
\alpha<1 alors le discriminant est négatif et on obtient 2 solutions complexes pour \mathbf r et une solution sinusoïdale amortie exponentiellement pour \mathbf {v(t)}.alors

Amortissement faible, régime pseudo-périodique

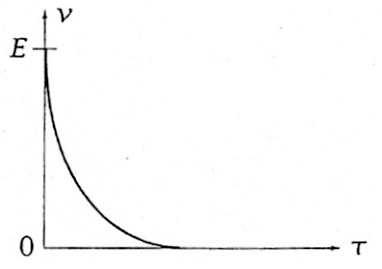
Pour \alpha = 1 (régime critique) on passe du régime apériodique au régime pseudo-périodique

Quand alors \alpha =1 alors \alpha = \frac{R}{2} \sqrt \frac{C}{L} = 1

La résistance critique est R_c = 2 \sqrt \frac{L}{C}

Le régime critique (pour lequel le discriminant est nul dans la question précédente) correspond au cas où le retour à l'équilibre (ici \mathbf {v=0} ) se fait le plus rapidement.