Question 1
Position d'équilibre :
exprimer la constante de raideur
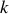 d'un ressort en fonction des données et la calculer.
d'un ressort en fonction des données et la calculer.
Question 2
Oscillations libres non amorties.
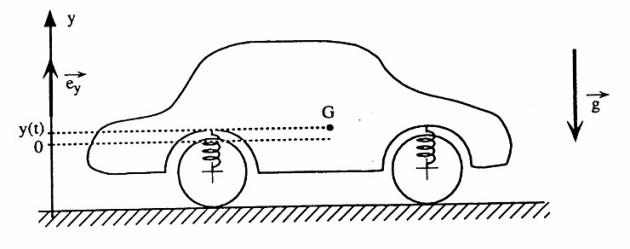
La figure 1 représente de manière simplifiée la voiture. Son mouvement est limité à une translation verticale et les quatre ressorts jouent un rôle identique. L'axe des
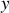 est dirigé suivant la verticale ascendante. On repère le centre de masse du véhicule par son abscisse
est dirigé suivant la verticale ascendante. On repère le centre de masse du véhicule par son abscisse
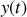 , l'origine des abscisses
, l'origine des abscisses
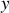 correspond à la position d'équilibre.
correspond à la position d'équilibre.
Déterminer l'équation différentielle satisfaite par la fonction
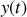 . En déduire la fréquence propre
. En déduire la fréquence propre
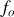 des oscillations du véhicule. Calculer
des oscillations du véhicule. Calculer
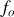 .
.
Question 3
Oscillations libres amorties.
Les oscillations précédentes nuisent au confort et à la stabilité du véhicule. L'utilisation de quatre amortisseurs identiques permet de limiter ou de supprimer ces oscillations. On suppose que chaque amortisseur exerce sur la châssis une force de frottement fluide
 où
où
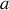 est une constante positive et
est une constante positive et
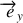 un vecteur unitaire de la verticale ascendante.
un vecteur unitaire de la verticale ascendante.
a). Montrer que l'équation différentielle satisfaite par la fonction
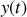 s'écrit :
s'écrit :

b) Donner l'expression de
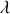 et de
et de
 .
.
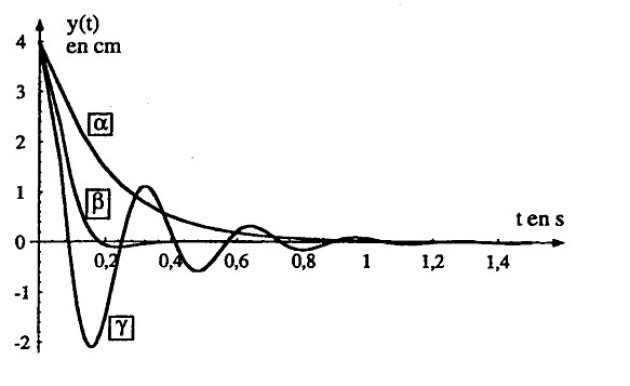
c) La figure 2 représente trois lois de variation
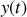 associées à trois valeurs
associées à trois valeurs
 ,
,
 et
et
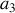 du coefficient d'amortissement
du coefficient d'amortissement
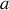 :
:
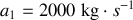 ,
,
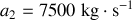 et
et
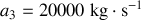 . Faire correspondre, en justifiant la méthode utilisée, chaque courbe
. Faire correspondre, en justifiant la méthode utilisée, chaque courbe
 ,
,
 et
et
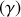 avec son coefficient d'amortissement (aucun calcul n'est demandé).
avec son coefficient d'amortissement (aucun calcul n'est demandé).
d) Parmi les trois valeurs proposées pour le coefficient d'amortissement, quelle est celle qu'il convient de choisir pour le confort et la sécurité des passagers ? justifier ce choix.