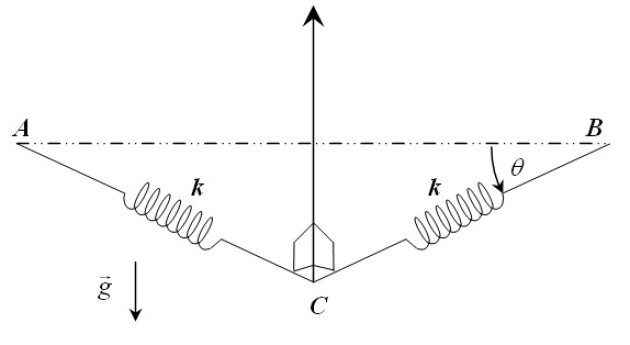
Le système précédemment décrit peut schématiser (grossièrement) un arc, la masse
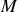représentant l'action de l'archer sur la corde (voir figure 2). L'arc est utilisé pour propulser parfaitement verticalement une flèche de masse
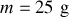. La flèche est posée en
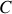et l'angle initial imposé par l'archer entre
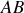et
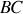est de
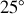. On négligera la variation de l'accélération de la pesanteur avec l'altitude et on la prendra égale à
.
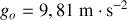Question 1
Déterminer la valeur
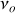de la vitesse de départ de la flèche. On considérera que la flèche quitte la corde lorsque le point
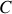passe sur la droite
.
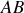Question 2
Dans cette question, on supposera tout frottement négligeable.
a) Déterminer l'altitude maximale
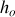atteinte par la flèche. On prendra une altitude nulle pour la droite
.
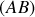b) Avec quelle précision relative peut-on supposer que l'accélération de la pesanteur est uniforme et de valeur
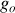? On donne le rayon de la Terre :
.
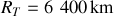Question 3
Dans cette question on suppose que la flèche est soumise à des frottements fluides du type
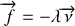où est la vitesse de la flèche. On appellera
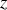l'altitude de la flèche à l'instant t sachant qu'initialement celle-ci est nulle.
a) Déterminer la vitesse de la flèche en fonction du temps. On introduira une grandeur
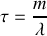. Indiquer l'unité de
.
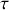b) Montrer, qu'à la retombée, la flèche ne peut dépasser une vitesse limite
.
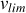c) Exprimer l'altitude z de la flèche en fonction du temps et de
,
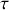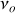et
.
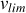d) La valeur de
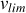est de
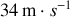. Déterminer l'altitude maximale notée
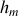atteinte par la flèche ainsi que la valeur du coefficient de frottement
.
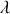e) Montrer que le travail fourni par la force de frottement
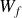est négatif. Qu'advient-il de cette grandeur énergétique ?
f) En effectuant un bilan énergétique sur un système que l'on définira clairement, déterminer le travail fourni par la force de frottement au cours de la phase ascensionnelle en fonction de
,
,
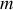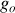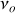et
.
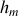