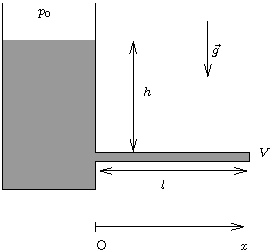
Un réservoir cylindrique vertical de grande section alimente une canalisation cylindrique horizontale, de section intérieure faible et uniforme.
La canalisation horizontale est de grande longueur
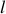. Elle est fermée, à son extrémité
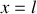, par une vanne
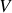. La hauteur d'eau dans le réservoir au dessus de la conduite est
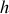. On ouvre complètement la vanne à
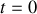. On admet que, pendant la durée du régime transitoire dans la conduite,
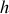ne varie pratiquement pas. L'écoulement de l'eau dans la conduite est supposé unidimensionnel (vitesse uniforme
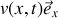sur chaque section droite). L'eau sera assimilée à un fluide parfait, homogène et incompressible, de masse volumique
.
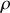On admettra que l'équation d'Euler peut se mettre sous la forme :
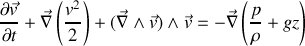
Question 1
Soient deux points
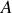et
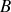d'une ligne de courant
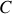à un instant
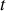donné. Multiplier scalairement l'équation (1) par un petit déplacement
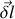le long de
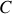et intégrer. Etablir que :
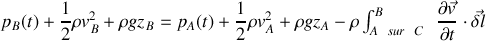
Question 2
Que dire de la vitesse de l'eau le long de la conduite, à un instant donné ? Etablir l'expression de la pression
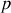de l'eau à l'instant
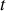, sur une section droite d'abscisse
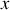, en fonction de la pression atmosphérique
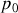et de
,
,
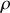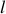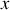et
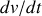dans la conduite.
Question 3
On fera l'approximation que l'on est en régime stationnaire dans tout le réservoir. Justifier brièvement cette approximation et établir l'équation différentielle vérifiée par
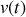. La résoudre en posant :
Question 4
Le régime permanent atteint, on ferme rapidement la vanne
à partir de l'instant
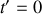; la vitesse de l'écoulement en
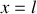variant selon la loi :
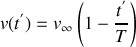
où
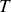est la durée de fermeture. Déterminer la pression
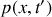dans la conduite pour
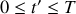. Déterminer en quel point et à quel instant cette pression est maximale.
Remarque :
Les questions 3. et 4. sont indépendantes.
