On considère un navire dont la coque très allongée a une section triangulaire. On se propose d'étudier le problème de la stabilité de cette coque par rapport au roulis dans un plan perpendiculaire à l'axe du navire.
La coque est constituée de deux plaques minces homogènes de largeur
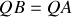 formant un dièdre droit, et de masse volumique uniforme. Ces plaques sont les seules parties pesantes du navire dont la masse totale par unité de longueur est
formant un dièdre droit, et de masse volumique uniforme. Ces plaques sont les seules parties pesantes du navire dont la masse totale par unité de longueur est
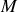 . La profondeur de la coque est
. La profondeur de la coque est
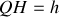 . La masse volumique de l'eau est
. La masse volumique de l'eau est
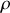 .
.
Le vent exerce un couple sous l'effet duquel le navire penche vers la gauche d'un angle
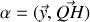 mesuré autour de
mesuré autour de
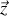 . On pose
. On pose
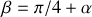 . On considère que le pont
. On considère que le pont
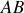 est toujours hors de l'eau. La partie immergée du bateau a pour section droite le triangle
est toujours hors de l'eau. La partie immergée du bateau a pour section droite le triangle
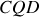 . On prend pour origine le point
. On prend pour origine le point
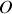 situé au niveau de la surface de l'eau à la verticale de
situé au niveau de la surface de l'eau à la verticale de
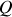 . L'eau est au repos. Une coupe du navire dans son plan de symétrie est représentée sur la figure 3.
. L'eau est au repos. Une coupe du navire dans son plan de symétrie est représentée sur la figure 3.
Question 1
Exprimer
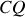 et
et
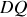 en fonction de
en fonction de
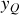 et de l'angle
et de l'angle
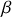 où
où
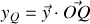 .
.
Question 2
Calculer de deux manières différentes la résultante des efforts extérieurs sur le navire.
Question 3
En déduire :
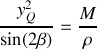
Question 4
Calculer les coordonnées du centre de gravité
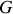 du navire dans le repère
du navire dans le repère
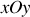 .
.
Question 5
Calculer les coordonnées du centre de poussée
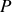 du navire dans le repère
du navire dans le repère
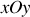 .
.
Question 6
A quelle condition la somme de la pesanteur et de la poussée d'Archimède tend-elle à redresser le navire ? Comment s'exprime cette condition lorsque
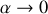 ?
?




