Réponse 1
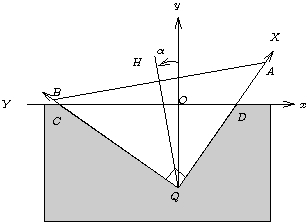
Une ligne de courant est par définition une ligne en tout point tangente au champ de vitesse. Elle ne correspond en général pas au trajet suivi par une particule fluide au cours du temps. On peut toutefois montrer qu'il y a coïncidence en régime permanent. En intégrant la relation (1) le long d'un chemin quelconque allant d'un point
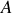 à un point
à un point
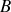 , on obtient :
, on obtient :
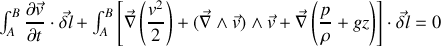
soit,
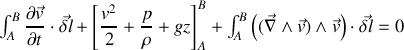
Si maintenant on impose au trajet
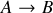 d'être une ligne de courant
d'être une ligne de courant
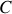 ,
,
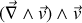 est orthogonal à la vitesse et donc au vecteur déplacement élémentaire
est orthogonal à la vitesse et donc au vecteur déplacement élémentaire
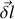 . Il s'ensuit que :
. Il s'ensuit que :
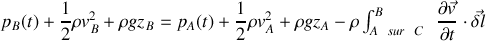
qui généralise la relation de Bernouilli à un régime dépendant du temps.
Réponse 2
Le fluide étant incompressible, le débit massique à travers la conduite se conserve et ce, même lors du régime transitoire. Comme la conduite est de section constante, on en déduit que
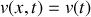 . On peut en donner une preuve plus formelle mais équivalente : la relation de conservation de la masse (ou relation de continuité) s'écrit :
. On peut en donner une preuve plus formelle mais équivalente : la relation de conservation de la masse (ou relation de continuité) s'écrit :
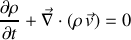
Comme
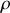 est constante, on a
est constante, on a
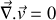 avec
avec
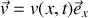 . D'où
. D'où
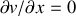 . Ainsi, la vitesse le long de la conduite ne dépend que du temps.
. Ainsi, la vitesse le long de la conduite ne dépend que du temps.
Considérons une ligne de courant joignant deux points de la conduite
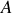 et
et
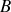 . On peut écrire, d'après ce qui précède :
. On peut écrire, d'après ce qui précède :
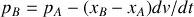 . Si l'on prend
. Si l'on prend
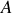 au niveau de la vanne où règne une pression
au niveau de la vanne où règne une pression
 , on a
, on a
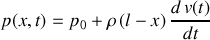
Réponse 3
Prenons une ligne de courant allant d'un point
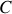 de la surface libre jusqu'au point
de la surface libre jusqu'au point
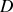 d'abscisse
d'abscisse
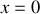 situé à l'entrée de la conduite (voir figure 4). On aura alors,
situé à l'entrée de la conduite (voir figure 4). On aura alors,
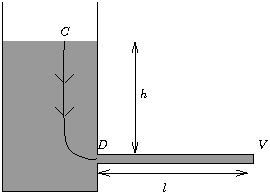
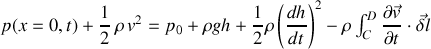
Compte tenu de l'expression établie à la question précédente, il vient :
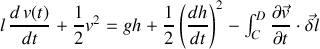
Nous allons montrer que l'on peut approximer cette égalité par
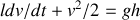 . Supposons pour cela que les sections du réservoir et de la conduite soient respectivement
. Supposons pour cela que les sections du réservoir et de la conduite soient respectivement
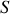 et
et
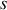 avec
avec
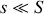 . La conservation du débit impose
. La conservation du débit impose
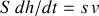 d'où
d'où
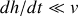 . On pourra donc négliger
. On pourra donc négliger
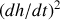 devant
devant
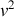 . De même, on a :
. De même, on a :
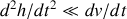 , ce qui permet de négliger
, ce qui permet de négliger
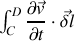 devant
devant
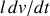 tant que
tant que
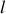 n'est pas trop petit (
n'est pas trop petit (
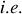 tant que l'on n'a pas
tant que l'on n'a pas
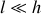 ). L'approximation du régime stationnaire dans le réservoir revient à négliger les variations de hauteur d'eau ainsi que les variations de vitesse d'écoulement dans le réservoir. On obtient alors l'équation différentielle vérifiée par
). L'approximation du régime stationnaire dans le réservoir revient à négliger les variations de hauteur d'eau ainsi que les variations de vitesse d'écoulement dans le réservoir. On obtient alors l'équation différentielle vérifiée par
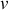 dans la conduite :
dans la conduite :
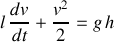
Dans la limite
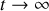 , la vitesse tend vers une constante
, la vitesse tend vers une constante
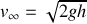 (régime permanent). Il s'agit donc de résoudre :
(régime permanent). Il s'agit donc de résoudre :
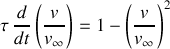
qui est à variables séparées. Puisque
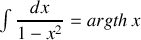
la vitesse a pour expression :
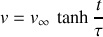
Réponse 4
Si la vanne est fermée, la pression en
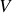 n'est plus connue a priori et ne peut plus servir de référence. On a toujours :
n'est plus connue a priori et ne peut plus servir de référence. On a toujours :
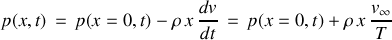
La pression au point
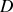 peut se calculer comme à la question précédente en considérant la ligne de courant
peut se calculer comme à la question précédente en considérant la ligne de courant
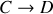 . L'hypothèse du régime stationnaire dans le réservoir tient toujours. Elle permet d'écrire :
. L'hypothèse du régime stationnaire dans le réservoir tient toujours. Elle permet d'écrire :
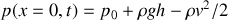 , d'où
, d'où
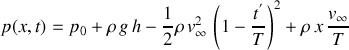
Calculons les dérivées partielles de la pression :
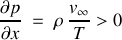
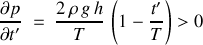
La pression est maximale en
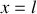 à l'instant
à l'instant
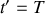 .
.
Complément :
La relation fondamentale régissant la dynamique d'une particule fluide s'écrit :
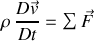 volumiques appliquées à la particule fluide,
volumiques appliquées à la particule fluide,
où
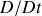 est un opérateur désignant la dérivée particulaire (ou convective ou encore advective) :
est un opérateur désignant la dérivée particulaire (ou convective ou encore advective) :
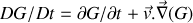 , qui permet d'obtenir l'évolution de la quantité
, qui permet d'obtenir l'évolution de la quantité
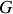 (scalaire ou vectorielle) tout en suivant le mouvement du fluide dont la vitesse est
(scalaire ou vectorielle) tout en suivant le mouvement du fluide dont la vitesse est
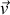 (voir les rappels de cours). Cette relation fondamentale est valable même si le fluide est compressible.
(voir les rappels de cours). Cette relation fondamentale est valable même si le fluide est compressible.
En particulier, le terme de gauche s'écrit bien
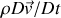 et non
et non
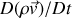 comme pourrait le suggérer une analogie trop rapide avec la mécanique du point. Le terme de droite fait intervenir, outre des forces volumiques comme la pesanteur ou la pression, des forces de viscosité ainsi que des forces liées à la compressibilité du liquide. Ici, le fluide est supposé incompressible et non visqueux, ce qui permet d'écrire
comme pourrait le suggérer une analogie trop rapide avec la mécanique du point. Le terme de droite fait intervenir, outre des forces volumiques comme la pesanteur ou la pression, des forces de viscosité ainsi que des forces liées à la compressibilité du liquide. Ici, le fluide est supposé incompressible et non visqueux, ce qui permet d'écrire
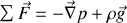 . En tenant compte de
. En tenant compte de
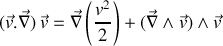
on obtient la relation (1) donnée dans l'énoncé.




