Réponse 1
Notons que
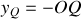 . Puisque
. Puisque
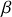 est l'angle que fait la verticale avec la droite (
est l'angle que fait la verticale avec la droite (
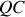 ), on a simplement :
), on a simplement :
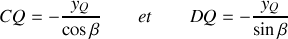
Réponse 2
Recensons les efforts extérieurs agissant sur l'unité de longueur du navire. Il y a tout d'abord son poids
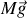 . Il y a ensuite la poussée d'Archimède que l'on peut calculer de deux manières. Nous considérerons dans tout ce qui suivra que la masse volumique de l'air est négligeable devant celle de l'eau (
. Il y a ensuite la poussée d'Archimède que l'on peut calculer de deux manières. Nous considérerons dans tout ce qui suivra que la masse volumique de l'air est négligeable devant celle de l'eau (
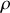 ), de telle sorte que la seule force de poussée provient de l'eau.
), de telle sorte que la seule force de poussée provient de l'eau.
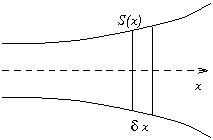
Première méthode : application du théorème d'Archimède. Il s'applique bien ici puisque si l'on remplace la section
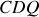 du navire par de l'eau, on obtient un état d'équilibre pour le fluide. Le navire reçoit du fluide porteur une poussée dont l'intensité est égale au poids du volume d'eau déplacé et de sens contraire. Par unité de longueur du bateau, le volume en question se réduit à la surface du triangle rectangle
du navire par de l'eau, on obtient un état d'équilibre pour le fluide. Le navire reçoit du fluide porteur une poussée dont l'intensité est égale au poids du volume d'eau déplacé et de sens contraire. Par unité de longueur du bateau, le volume en question se réduit à la surface du triangle rectangle
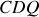 , et la force vaut :
, et la force vaut :
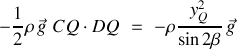
Deuxième méthode : calcul direct en intégrant les forces élémentaires de pression. Sur un élément de longueur
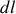 de la coque, s'applique une force
de la coque, s'applique une force
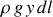 normale à la paroi (la pression atmosphérique ne contribue pas car elle est isotrope). La composante de cette force suivant (
normale à la paroi (la pression atmosphérique ne contribue pas car elle est isotrope). La composante de cette force suivant (
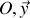 ) est
) est
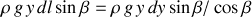 sur la partie (
sur la partie (
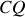 ) et
) et
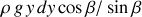 sur la partie (
sur la partie (
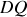 ). En projetant la force de poussée sur l'axe (
). En projetant la force de poussée sur l'axe (
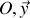 ) (à l'équilibre, la composante de la force de poussée selon l'axe (
) (à l'équilibre, la composante de la force de poussée selon l'axe (
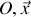 ) est nulle), il vient :
) est nulle), il vient :
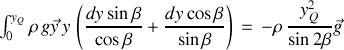
Les deux méthodes sont bien entendu équivalentes mais la seconde est plus générale car elle reste valable même lorsque le théorème d'Archimède ne s'applique plus. La résultante
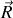 des efforts extérieurs est :
des efforts extérieurs est :
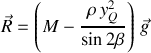
Réponse 3
On suppose que le centre de gravité du navire n'est soumis à aucune accélération : la résultante des forces agissant sur le navire est nulle, ce qui permet d'écrire :
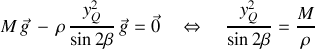
En d'autres termes le volume immergé reste constant : de tels mouvements sont appelés isocarènes.
Réponse 4
Le centre de gravité
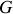 se trouve sur l'axe de symétrie (
se trouve sur l'axe de symétrie (
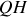 ) puisque la coque est homogène. Considérons les points milieux de
) puisque la coque est homogène. Considérons les points milieux de
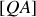 et
et
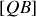 . G se trouve au milieu du segment formé par les deux points précédents (le barycentre est associatif). Ces deux points sont distants de
. G se trouve au milieu du segment formé par les deux points précédents (le barycentre est associatif). Ces deux points sont distants de
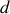 où
où
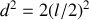 (on a posé
(on a posé
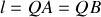 ). Avec le théorème de Pythagore, il vient :
). Avec le théorème de Pythagore, il vient :
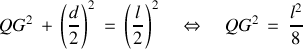
soit encore :
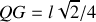 . On aurait pu retrouver ce résultat en revenant à la définition du centre de gravité et en écrivant :
. On aurait pu retrouver ce résultat en revenant à la définition du centre de gravité et en écrivant :
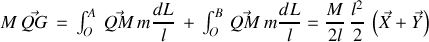
d'où
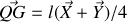 .
.
Enfin, un vecteur unitaire de l'axe (
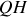 ) est
) est
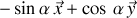 . On a donc :
. On a donc :
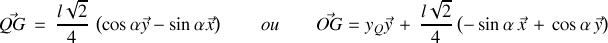
Réponse 5
Le centre de poussée est par définition le centre de masse du fluide déplacé. Il ne s'agit en général pas d'un point fixe du solide immergé.
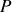 est donc le centre de gravité du triangle (
est donc le centre de gravité du triangle (
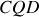 ) : il se trouve au point de concours des médianes. Soit
) : il se trouve au point de concours des médianes. Soit
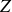 le milieu du segment
le milieu du segment
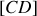 ; on a
; on a
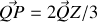 , puis
, puis
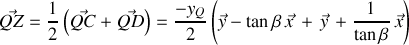
et
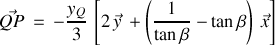
En conclusion :
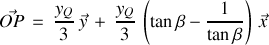
Réponse 6
Remarquons pour commencer que la poussée d'Archimède, qui s'oppose au poids d'après la question II.3., s'applique au centre de poussée
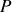 , alors que le poids s'applique au centre de gravité
, alors que le poids s'applique au centre de gravité
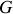 . Ces deux forces exercent un couple qui peut redresser ou faire chavirer l'embarcation.
. Ces deux forces exercent un couple qui peut redresser ou faire chavirer l'embarcation.
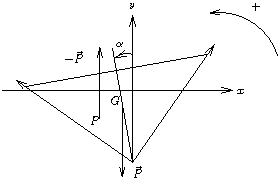
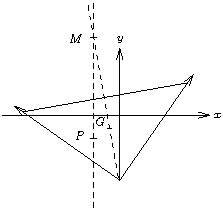
Considérons que le bateau penche vers la gauche, comme sur la figure 5. Pour que la somme de la pesanteur et des efforts de poussée d'Archimède tende à redresser le navire, il faut se trouver dans la situation de la figure où le moment des forces tend à induire une rotation vers la droite. Il faut donc avoir
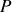 à gauche de
à gauche de
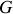 . En effet, le moment en
. En effet, le moment en
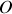 des forces exercées sur le navire est :
des forces exercées sur le navire est :
![]()
La projection de ce moment sur la direction
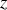 doit être, dans la situation de la figure 5, négatif afin de redresser le navire, ce qui se traduit par
doit être, dans la situation de la figure 5, négatif afin de redresser le navire, ce qui se traduit par
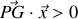
avec les conventions d'orientation de la figure 5. De façon plus générale,
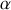 étant positif suivant nos conventions d'orientation, la condition de stabilité s'écrit :
étant positif suivant nos conventions d'orientation, la condition de stabilité s'écrit :
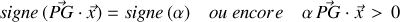
avec
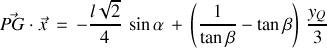
Que devient cette expression lorsque
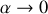 ? Effectuons des développements limités au premier ordre en
? Effectuons des développements limités au premier ordre en
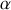 des différentes quantités qui nous intéressent :
des différentes quantités qui nous intéressent :
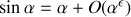
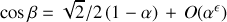
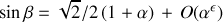
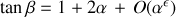
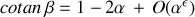
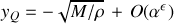
On en déduit la condition de stabilité des petits déplacements :
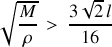
Si elle est satisfaite, le navire peut osciller autour de sa position d'équilibre
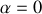 et ne pas chavirer. A
et ne pas chavirer. A
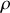 et
et
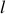 fixés, le bateau est d'autant plus stable qu'il est lourd. Bien entendu, s'il est trop lourd, il coule ! La condition de flottaison s'écrit
fixés, le bateau est d'autant plus stable qu'il est lourd. Bien entendu, s'il est trop lourd, il coule ! La condition de flottaison s'écrit
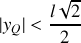
soit encore, puisque l'on s'intéresse à la position d'équilibre
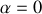 :
:
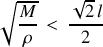
Complément :
les problèmes de stabilité de bateaux se formalisent en introduisant la notion de métacentre. Par définition, le métacentre
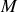 est l'intersection de la verticale passant par le centre de poussée
est l'intersection de la verticale passant par le centre de poussée
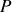 et de l'axe de symétrie passant par
et de l'axe de symétrie passant par
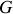 (voir la figure 6).
(voir la figure 6).
Définissons une mesure algébrique sur (
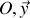 ) :
) :
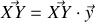 . Une condition nécessaire et suffisante pour que l'équilibre soit stable
. Une condition nécessaire et suffisante pour que l'équilibre soit stable
est que
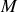 soit au dessus de
soit au dessus de
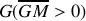 . On peut montrer que
. On peut montrer que
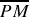 est toujours positif. Or
est toujours positif. Or
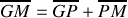 . Ainsi, une condition suffisante de stabilité de l'équilibre est :
. Ainsi, une condition suffisante de stabilité de l'équilibre est :
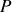 au dessus de
au dessus de
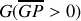 . Cette dernière condition est assez intuitive mais relativement restrictive. En effet, dans l'exercice que nous venons de traiter :
. Cette dernière condition est assez intuitive mais relativement restrictive. En effet, dans l'exercice que nous venons de traiter :
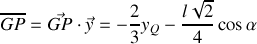
et pour les petits déplacements :
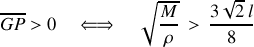
Nous pouvons conclure que pour
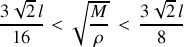
le navire est stable mais le centre de poussée
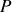 est en dessous du barycentre
est en dessous du barycentre
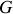 .
.




