Soit une distribution de charge de densité volumique
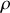, créant un potentiel
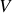et un champ
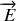. La généralisation au cas continu des résultats du paragraphe précédent permet de définir l'énergie électrostatique de la distribution de charges
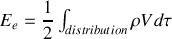
En utilisant la densité d'énergie électrique
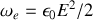, on peut réécrire
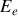sous la forme
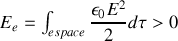
Attention :
Les deux expressions diffèrent par le domaine d'intégration.
Dans le cas de deux distributions de charges (1) et (2), l'application du principe de superposition permet de définir l'énergie d'interaction mutuelle
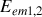des deux distributions :
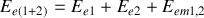
avec
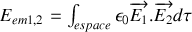
Contrairement à l'énergie électrostatique de chaque distribution, cette énergie mutuelle est de signe quelconque.
