On se propose de modéliser la croissance d'une couche de glace à la surface d'un lac gelé.
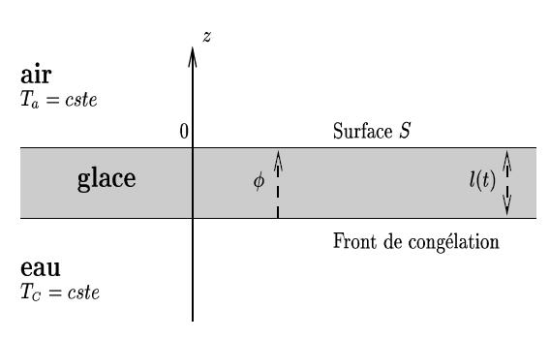
L'eau du lac est supposée à la température constante T_c (température de congélation), et est recouverte d'une couche de glace d'épaisseur l(t), la glace occupant la région -l(t)<z < 0. Le temps est noté t.
L'air, au dessus de la glace, est à la température T_a constante. On notera que la température T_a de l'air est inférieure à la température T_c de l'eau.
La chaleur produite par la solidification de l'eau à l'interface eau-glace est conduite jusqu'à la surface S (voir la figure) où elle est libérée dans l'air.
La température de la glace vaut T_C en z=-l(t) et vaut T_S(t) pour z=0. Cette température T_S(t) dépend du temps t et est différente en général de la température T_a de l'air. Entre la glace et l'air, il existe des échanges de type convectif, et le contact, non parfait, est modélisé par la donnée d'un coefficient d'échange h (on ne confondra pas avec le coefficient calorimétrique).
On admet que dans la couche de glace, la température T ne dépend que de t et de z. De plus, on adopte l'hypothèse dite de "quasi-stationnarité", c'est-à-dire que l'on néglige les variations de T avec le temps devant ses variations spatiales : autrement dit, l'équation pour la température T(z,t) s'écrit (voir la partir relative à la conduction de la chaleur dans la section G des rappels de cours de thermodynamique) :
\frac{\partial^2T}{\partialz^2}=0.
Le but de ce problème est de déterminer l(t) et T_S(t).
\rho_g, masse volumique de la glace,
\lambdag, conductivité thermique de la glace,
Lg, chaleur latente de la glace,
h, coefficient d'échange air-glace défini par la relation
\overrightarrowq\cdot \overrightarrowz=h(T_S(t)-T_a).
\rhog=900kg\cdotm^{-3},\qquad\qquad\lambda_g=2,1W\cdotm^{-1}\cdotK^{-1}
Lg=3,3\,10^5W\cdotkg^-1\cdot s,\qquad \qquadh=50W\cdotm^{-2}\cdotK^{-1}
T_C= 273 K,\qquad \qquad\qquadT_a=253 K.