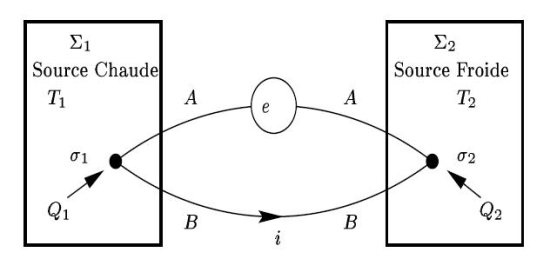
Le système étudié est un couple thermoélectrique, c'est-à-dire deux fils, l'un en métal A et l'autre en métal B, soudés à leurs extrémités.
Les soudures \sigma_1 et \sigma_2 entre les deux extrémités de chaque fil A et B sont plongées dans deux sources de chaleur différentes :
-
\sigma_1 est plongée dans \Sigma_1 à la température T_1,
-
\sigma_2est plongée dans le thermostat \Sigma_2 à la température T_1.
Il existe un courant "spontané" i entre les soudures, et une force électromotrice "spontané" e que l'on mesure grâce à un voltmètre.
On constate également :
-
une absorption de chaleur Q_1>0 par la soudure \sigma_1 (aux dépens de \Sigma_1) ;
-
un dégagement de chaleur Q_2<0 par \sigma_2 (au profit de \Sigma_2).
Si pendant une seconde, une soudure \sigma_n entre un métal A et un métal B à la température T est traversée par un courant i, de A vers B, elle échange avec le milieu extérieur une quantité de chaleur Q_n=iV_{AB}(T). C'est l'effet PELTIER, et V_{AB}(T) est nommée f.e.m. PELTIER.
Le signe de la chaleur échangée dépend de la nature des métaux et du sens du courant. V_{AB}(T)=V_{BA}(T) et le signe dépend de la nature de A et de B. L'échange de chaleur au niveau des soudures étant isotherme, l'effet PELTIER est réversible.
On considérera dans cette première partie que l'effet THOMSON, étudié dans la seconde partie, est négligeable. De même, on ne prendra pas en considération la conduction de la chaleur par les fils, et l'effet JOULE dû à leur résistance.
Question 1
Quel est le signe de V_{AB}(T)?
Question 2
Faire le bilan des échanges de chaleur survenant par seconde entre :
-
le thermocouple et \Sigma_1,
-
le thermocouple et \Sigma_2.
Question 3
Faire le bilan des échanges de travail électrique survenant par seconde entre le générateur "thermocouple" et l'extérieur (le voltmètre).
Question 4
L'ensemble des transformations étudiées constitue un cycle. Déduire de l'application du premier principe de la thermodynamique au système "thermocouple" une expression de e en fonction de V_{AB}(T_1) et V_{AB}(T_2).
Question 5
Exprimer la variation d'entropie du système par seconde. En déduire une relation entre V_{AB}(T_1), T_1, V_{AB}(T_2) et T_2.
Question 6
\Sigma_2 est assimilable à un thermostat : T_2 reste constant. T_1 est en revanche susceptible de varier : dériver l'équation trouvée au 5. par rapport à cette variable T_1. Poser ensuite : T=T_1 et en déduire une expression de la f.e.m. V_{AB}(T) en fonction de T et d'un coefficient de proportionnalité \alpha dont on précisera le signe.
Question 7
Donner l'expression de e en fonction de \alpha, T_1, T_2. Connaissant le signe de \alpha, que peut-on dire de l'évolution de e en fonction de \DeltaT=T_1-T_2 ?
Question 8
Donner l'expression du rendement \eta_o=-W/Q_1 de ce moteur thermique. Peut-on le comparer au rendement de CARNOT ? Si oui, expliquer pourquoi.