Équations horaires du mouvement
Ce sont les fonctions
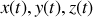ou
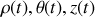
Exemple n°1 (en cartésienne) :
;
;
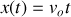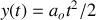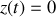
Exemple n°2 (en cartésienne, dans le plan xOy) :
;
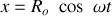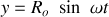
Exemple n°3 (en cylindrique) :
;
;
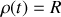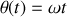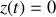
Équation de la trajectoire
C'est la relation liant
,
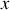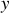et
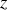ou liant
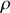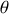et
et
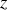indépendamment du temps. Cette équation est obtenue en éliminant le temps entre les différentes coordonnées ou équations horaires.
Exemple n°1 : Pour tout
,
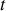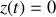: le mouvement se fait dans le plan
.
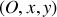On élimine le temps
:
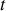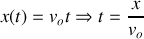et
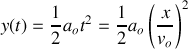
L'équation de la trajectoire est
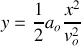: (mouvement parabolique dans le plan
)
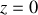Exemple n°2 :
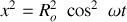et
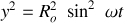soit :
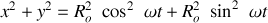
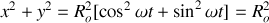
La trajectoire correspond à un cercle de rayon
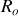et de centre
.
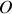Exemple n°3 : Pour tout
,
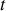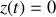: le mouvement se fait dans le plan
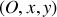. Pour tout
,
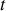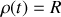(une constante) : Ceci correspond, en coordonnées polaires, à l'équation d'un cercle de centre
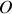et de rayon
.
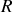Équation différentielle
C'est une équation reliant une fonction (par exemple
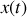)avec ses dérivées.
Exemples :
;
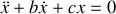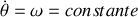; etc...
