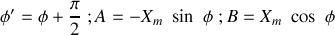Dans le référentiel d'étude, la trajectoire est une portion de droite. On choisit un axe
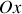suivant cette droite et le point
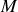est repéré par son abscisse. L'équation horaire correspond à
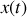et la trajectoire est connue. Il y a une seule composante pour les vecteurs vitesse (
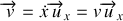) et accélération (
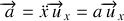). Si le choix est laissé, on prend souvent l'origine
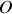confondue avec la position du point
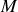à l'instant
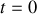(condition initiale).
Mouvement rectiligne uniforme
Définition :
Vecteur vitesse constant
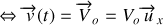
Équation différentielle :
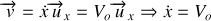
Accélération nulle :
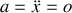
Équation horaire :
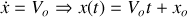(primitive d'une constante)
Les conditions initiales permettent de déterminer les constantes d'intégration comme ici
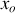. Avec la condition initiale
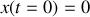on obtient
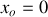et l'équation horaire devient :
.
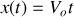Mouvement rectiligne uniformément varié
Définition :
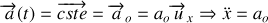et trajectoire rectiligne.
L'équation différentielle du mouvement :
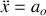
La vitesse : primitive de l'accélération :
(
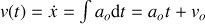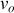constante d'intégration)
L'équation horaire
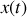s'obtient par intégration de la vitesse
:
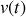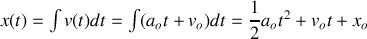
Les constantes
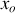et
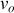sont déterminées par 2 conditions ou par les conditions initiales (conditions à
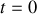). Par exemple, si à
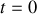, le point
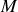est en
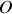sans vitesse, on aura les conditions
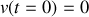et
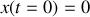. En reportant dans les expressions de la vitesse et position on obtient très simplement
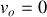et
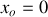. alors l'équation horaire devient
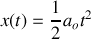
Attention :
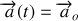vecteur constant ne suffit pas pour dire que le mouvement est rectiligne uniformément varié. En effet on a alors :
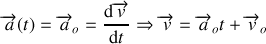. Si le vecteur vitesse
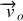à
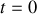n'est pas suivant la direction du vecteur accélération le mouvement sera plan, dans le plan contenant
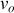et
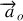(voir par exemple le mouvement de chute parabolique). Il faut donc rajouter une condition : soit dire que le mouvement est rectiligne soit préciser qu'à un instant
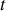quelconque vecteur accélération et vecteur vitesse sont colinéaires.
Remarque :
Le mouvement est uniformément accéléré si la norme du vecteur vitesse est une fonction croissante de
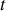, soit
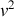fonction croissante. La dérivée de
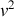doit donc être positive. La condition sera :
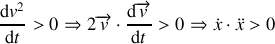
Remarque :
En exprimant le temps
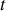en fonction de la vitesse et en reportant dans l'expression de
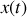il est possible d'obtenir une relation entre position et vitesse indépendamment du temps :
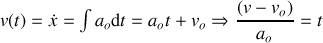
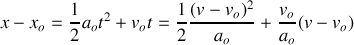
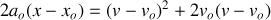
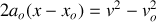
Mouvement rectiligne quelconque
L'accélération est une fonction quelconque du temps. En intégrant une première fois cette fonction, on obtient la vitesse à une constante près. En l'intégrant une deuxième fois on obtient l'équation horaire.
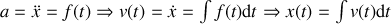
Les constantes d'intégration se déterminent suivant les conditions initiales (vitesse et position à
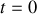) ou à un instant t quelconque.
Mouvement rectiligne sinusoïdal
Définition :
L'équation horaire est une fonction sinusoïdale du temps du type :
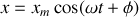
C'est le mouvement par exemple d'une masse accrochée à un ressort.
La quantité
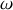s'appelle la pulsation (unité en
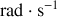, homogène à l'inverse d'un temps).
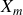est l'amplitude maximale du mouvement d'oscillation du point
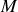autour du point
.
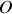La fonction cosinus variant entre
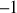et
,
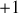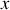oscille entre
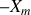et
.
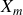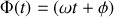est la phase à l'instant
.
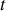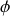est la phase à l'origine (à
)
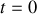La fonction cosinus est une fonction périodique de période
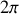. Si
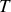est la période temporelle du mouvement, on aura donc :
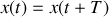soit
.
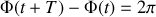Cela conduit à :
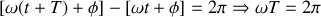
La fréquence
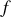correspond au nombre d'oscillations (d'aller et retour) par seconde. On a donc
.
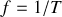La vitesse est obtenue en dérivant la fonction
:
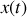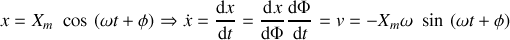
L'accélération est obtenue en dérivant la fonction
:
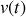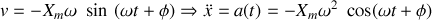
On constate que l'accélération peut s'exprimer en fonction de
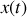. La relation est :
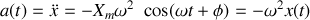
L'Équation différentielle du mouvement est donc :
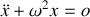
Ceci correspond à l'équation différentielle de l'oscillateur harmonique.
Remarque :
La solution de cette équation différentielle peut s'écrire de différentes façons, toutes équivalentes. On a :
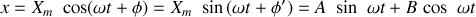
En utilisant les relations trigonométriques usuelles, on obtient très simplement :
