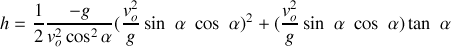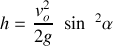Considérons le cas où le vecteur accélération est un vecteur constant et qu'à un instant choisi comme origine
 le vecteur vitesse
le vecteur vitesse
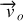 est connu.
est connu.
Pour simplifier l'étude, on peut définir le repère à partir des données du problème.
L'origine du repère : position du point à
L'axe
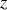 suivant le vecteur accélération, soit
suivant le vecteur accélération, soit
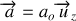
L'axe
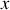 perpendiculaire à l'axe
perpendiculaire à l'axe
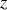 et dans le plan contenant
et dans le plan contenant
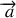 et
et
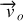 .
.
Pour
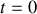 on a
on a
L'axe
 est défini de sorte que
est défini de sorte que
 forment une base orthonormée directe.
forment une base orthonormée directe.
On obtient par intégrations successives :
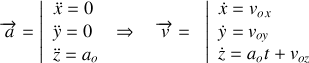 avec
avec
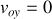
on a
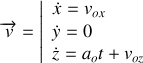
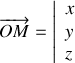 avec
avec
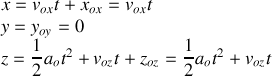
Dans le cas où
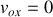 , on retrouve le mouvement rectiligne uniformément varié suivant l'axe des
, on retrouve le mouvement rectiligne uniformément varié suivant l'axe des
 .
.
Pour
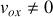 , le mouvement est un mouvement plan, dans le plan défini par le vecteur accélération et le vecteur vitesse à l'instant
, le mouvement est un mouvement plan, dans le plan défini par le vecteur accélération et le vecteur vitesse à l'instant
 .
.
Le mouvement projeté suivant l'axe des
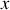 est un mouvement uniforme de vitesse
est un mouvement uniforme de vitesse
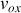 .
.
Le mouvement projeté suivant l'axe des
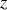 est uniformément varié, d'accélération constante
est uniformément varié, d'accélération constante
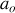 .
.
Equation de la trajectoire
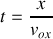 et
et
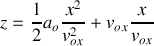
Si
 est l'angle que fait le vecteur vitesse
est l'angle que fait le vecteur vitesse
 avec l'axe des
avec l'axe des
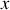 et
et
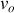 la norme de ce vecteur vitesse, on peut écrire :
la norme de ce vecteur vitesse, on peut écrire :
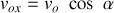 ;
;
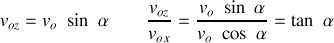
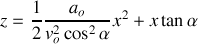
La trajectoire est une portion de parabole.
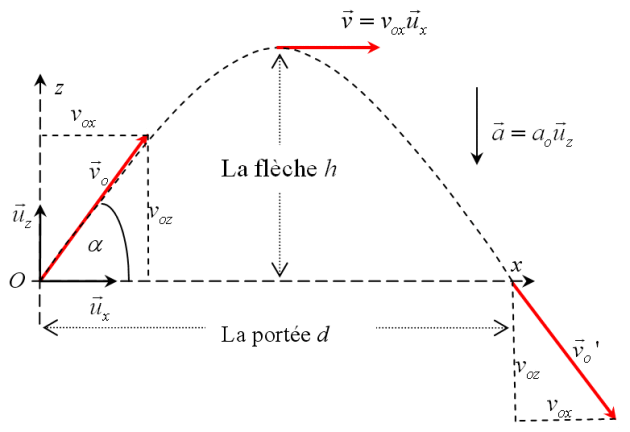
Figure 18 : Chute parabolique. L'accélération
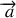 correspond ici à l'accélération de la pesanteur
correspond ici à l'accélération de la pesanteur
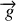 .
.
Le schéma de la figure 18 représente la trajectoire d'un projectile pour lequel le vecteur accélération vaut :
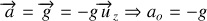 , où
, où
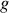 est l'accélération de la pesanteur.
est l'accélération de la pesanteur.
La flèche
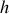 correspond à l'altitude maximale que peut atteindre le point mobile. La portée
correspond à l'altitude maximale que peut atteindre le point mobile. La portée
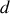 correspond à la distance maximale que peut atteindre le point lorsque qu'il revient à l'ordonnée
correspond à la distance maximale que peut atteindre le point lorsque qu'il revient à l'ordonnée
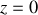 .
.
Calcul de la portée
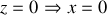 et
et
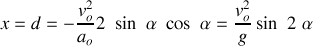
La portée est maximale pour
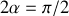 , soit pour un angle de tir correspondant à
, soit pour un angle de tir correspondant à
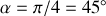 .
.
Calcul de la flèche
Elle peut être obtenue de différentes façons. On peut rechercher, par exemple, l'ordonnée correspondant à l'abscisse
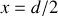 . On obtient alors :
. On obtient alors :