Enoncé de la 2ème loi de Newton
Considérons un système matériel
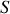, de centre d'inertie
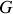, de masse
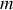, se déplaçant dans un référentiel Galiléen
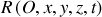. Si ce système n'est pas mécaniquement isolé, c'est à dire s'il subit une action non compensée, le principe d'inertie nous dit que sa quantité de mouvement ne peut pas être constante dans le temps.
Remarque :
Le principe (ou relation) fondamental(e) de la dynamique nous permet de lier la cause (actions non compensées) à l'effet observé (quantité de mouvement variable). Il s'écrit:
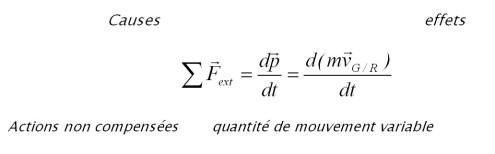
Attention :
La somme des forces extérieures appliquées à un système en translation dans un référentiel Galiléen est égale à la dérivée du vecteur quantité de mouvement du centre d'inertie de ce système.
Fondamental :
Comme la masse du système est supposée constante dans le temps, il en résulte que la relation fondamentale de la dynamique peut s'écrire sous la forme:
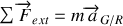
Ceci constitue le théorème du centre d'inertie:
Théorème :
Dans un référentiel galiléen, le mouvement du centre d'inertie d'un système matériel est le même que celui d'un point matériel coïncidant avec ce centre, point qui aurait comme masse la masse totale du système et auquel on appliquerait la somme des forces agissant sur le système.
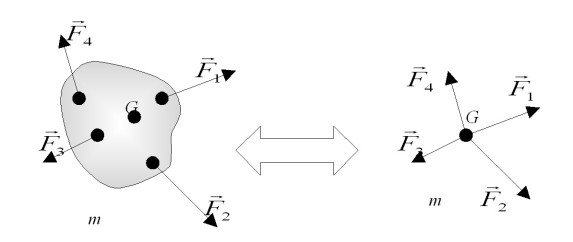
Par la suite, nous ne nous intéresserons qu'au mouvement du centre d'inertie d'un système (correspondant au mouvement d'ensemble du système). Toute les forces extérieures appliquées au système seront donc représentées en ce point (voir figure 4).
Ce que nous venons de décrire concerne le mouvement de translation du système. Des considérations formellement identiques vont nous permettre d'appréhender le mouvement de rotation d'un système.
Théorème du moment cinétique
Définition du moment cinétique
Considérons un point matériel
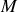en rotation autour d'un axe fixe
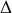dans un référentiel Galiléen
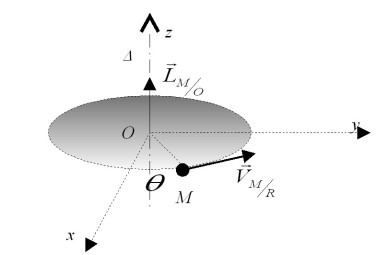
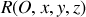(voir figure 5).
Définition :
On appelle moment cinétique du point
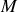par rapport à un point fixe
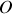de l'axe , le moment de sa quantité de mouvement que l'on note :
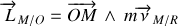
Le moment cinétique est donc un vecteur perpendiculaire à
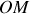et à la vitesse du point. C'est donc une grandeur perpendiculaire à la trajectoire du point
.
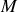Théorème du moment cinétique
Le théorème du moment cinétique est un théorème qui définit la valeur de la dérivée du moment cinétique. Dans le référentiel
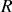Galiléen la dérivée du moment cinétique s'écrit:
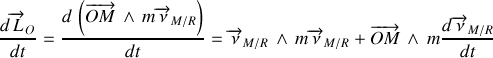
Il en résulte que la dérivée du moment cinétique est égale à la somme des moments des forces extérieures par rapport au point
:
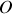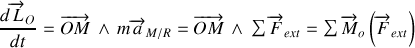
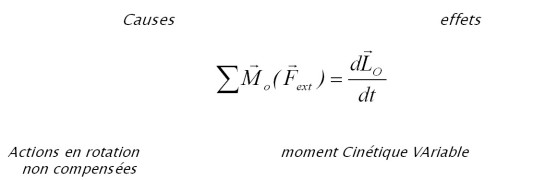
Théorème :
la dérivée du moment cinétique d'un point matériel en rotation autour d'un axe fixe passant par O est égale à la somme des moments des forces extérieures appliquées au système.
Remarque :
Si le système est en équilibre (pas de rotation) alors la somme des moments des forces extérieures est nulle et le moment cinétique est nul.
Pour un point matériel il est possible d'exprimer la dérivée du moment cinétique à l'aide du moment d'inertie
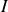, par rapport à l'axe de rotation choisi, de la masse
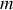. Le moment cinétique du point matériel est égal à:
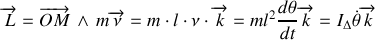
Par définition le moment d'inertie du point matériel distant de
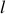de l'axe de rotation est égal au produit de la masse de ce point par le carré de la distance à l'axe de rotation :
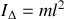
Il en résulte que:
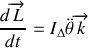
Remarque :
Pour un point matériel en rotation autour d'un axe fixe, on peut appliquer indifféremment le principe fondamental de la dynamique ou le théorème du moment cinétique.
