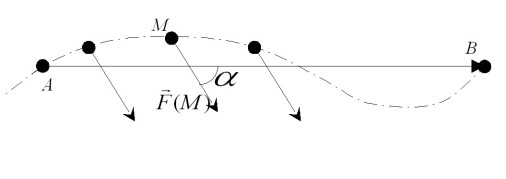
Dans le cas où le vecteur force reste constant (en norme, direction et sens) au cours du déplacement de son point d'application comme l'indique la figure 18, l'expression du travail de cette force se simplifie. Il est en effet possible de sortir ce vecteur de l'intégrale
Ce qui conduit à:
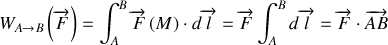
On constate alors que le travail de cette force ne dépend pas du chemin suivi mais uniquement de la position initiale (
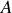) et finale (
).
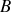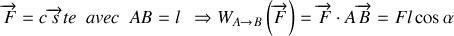
Un exemple classique de ce type de situation concerne le travail du poids d'un corps. Considérons une masse
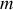se déplaçant d'un point
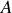d'altitude
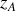à un point
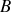d'altitude
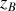et calculons le travail du poids de ce corps au cours de ce déplacement (voir figure 19). Le déplacement de
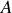à
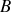est supposé quelconque c'est à dire que le chemin qui mène de
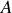à
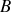peut prendre différentes trajectoires. Le poids
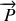est une force constante en norme et en direction (à la condition de rester dans une région de l'espace pas trop étendue, voir chapitre "Lois de Newton et référentiels").
On obtient donc pour le travail du poids :
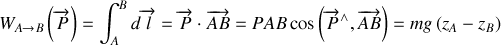
Remarque :
On constate que ce travail ne dépend pas du chemin suivi mais uniquement de la différence d'altitude. Il est positif (donc moteur) si l'altitude finale est plus petite que l'altitude initiale et négatif (donc résistant) dans le cas contraire.
Ce résultat peut être obtenu en utilisant les coordonnées des points
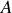et
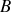et des composantes du vecteur
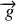dans un repère cartésien
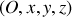. En orientant l'axe
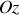vers le haut (voir figure 19) nous pouvons écrire :
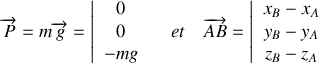
soit :
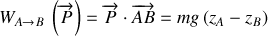
Enfin, ce résultat peut se retrouver en partant de l'expression du travail élémentaire du poids. Dans le repère cartésien
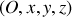, on peut écrire :
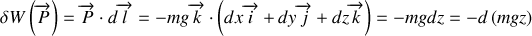
Il en résulte que pour aller de
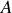en
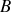, le travail du poids est donné par:
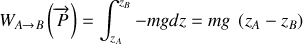
Remarque :
Le travail élémentaire de
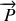correspond à l'opposé de la différentielle d'un fonction qui serait
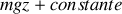. Nous y reviendrons par la suite.
