Considérons un ressort de raideur
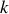, de longueur au repos
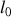, au bout duquel est accrochée une masse
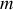comme l'indique la figure 20. Le ressort et la masse sont sur un plan horizontal et nous nous intéressons uniquement à la tension du ressort.
Remarque :
La force élastique
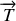, c'est à dire de la force de tension du ressort est une force qui varie avec l'état d'étirement du ressort
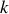. Ce n'est donc pas une force constante au cours du déplacement et pour calculer le travail de cette force il nous faut calculer le travail élémentaire de cette force sur un déplacement infiniment petit sur lequel nous considérerons que la force est constante.
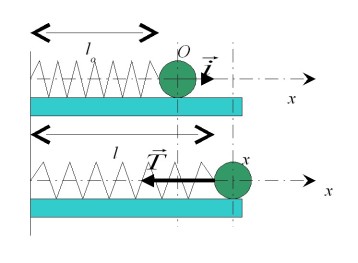
Avec les conventions de la figure 20, la tension s'exprime de la façon suivante :
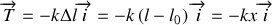
Le travail élémentaire de la force élastique
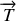, lorsque la masse passe d'une position
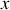à une position
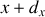, est donc donné par:
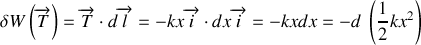
Lorsque le point d'application passe d'une position
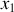à une position
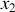, le travail de cette force est donc :
.
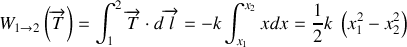Remarque :
Le travail de cette force ne dépend pas du chemin suivi mais uniquement de la position initiale et finale du ressort. Le travail élémentaire de
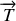correspond là aussi à l'opposé de la différentielle d'une fonction qui est
.
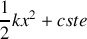