En reprenant les résultat obtenus dans le paragraphe " Travail d'une force constante : poids d'un corps", nous avons avec l'axe
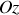, axe vertical ascendant :
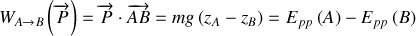
Par comparaison avec la relation intégrale, il apparaît clairement que nous pouvons définir la fonction énergie potentielle de pesanteur par :
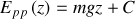
Cette fonction est définie à une constante
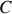près qu'il convient de fixer. La détermination de cette constante se fait par le choix arbitraire du zéro de la fonction énergie potentielle. En général, l'énergie potentielle de pesanteur est prise nulle en
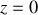ce qui impose
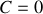. Ce choix entraîne que:
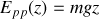
Remarque :
Le calcul de l'énergie potentielle de pesanteur se fait tout aussi simplement à partir de la relation différentielle :
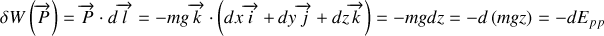
Nous obtenons immédiatement l'expression de la fonction énergie potentielle
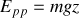, en choisissant la constante nulle comme précédemment.
Si l'axe
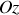est orienté vers le bas (axe vertical descendant) nous obtenons :
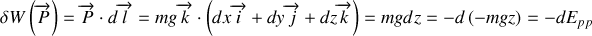
et l'expression de l'énergie potentielle de pesanteur devient :
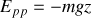
Complément :
Il faut donc bien préciser l'orientation choisie pour l'axe
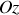pour utiliser la bonne expression de l'énergie potentielle. Un bon moyen de vérifier si l'expression utilisée est correcte consiste à vérifier que l'énergie potentielle de pesanteur augmente toujours avec l'altitude.
