La mécanique classique permet la description, au cours du temps, de mouvements de systèmes qui évoluent dans l'espace à 3 dimensions.
Pour cela, deux éléments sont nécessaires : un repère muni de son échelle de mesures (sa métrique) et un chronomètre.
Ce sont les deux éléments constitutifs d'un référentiel.
La description des mouvements s'appuie sur deux démarches complémentaires, chacune utilisant ses propres outils et apportant ses éléments de réponses.
La cinématique est construite autour des
éléments cinématiques suivants : position (et trajectoire), vitesse (et impulsion), accélération. Les moments de la vitesse et de l'accélération peuvent s'ajouter à la description.
Outre le repérage spatial, des informations sur la façon dont est parcourue la trajectoire sont déduites : sens de parcours, points de rebroussement...
La dynamique, plus complète, s'intéresse en plus à l'origine, à la source du mouvement : elle s'appuie sur les forces... et les moments de ces forces.
Elle fournit les lois qui associent d'une part, les éléments cinématiques précédents et d'autre part, les forces et moments.
Avec la richesse apportée par les forces, figure également la notion d'énergie que les forces véhiculent pendant le mouvement qu'elles produisent.
L'énergie constitue une troisième voie d'analyse : l'énergétique à l'origine des sciences appliquées.
Cette voie, assez peu exploitée en mécanique classique à cause de certaines limites, sera étoffée, enrichie dans le formalisme lagrangien et son principe de moindre action (grain 2).
Fondamental : En mécanique, quelle approche d'étude ?
Avant toute description et modélisation, les limites du système doivent être définies.
En effet, comme pour la thermodynamique, la démarche à suivre est balisée par les questions suivantes :
Quel est le système à étudier ? Quelles sont ses limites et comment les exprimer ? Quelles sont les conditions aux bords, les contraintes ? Conditions relatives à l'espace.
Quelles sont ses conditions initiales? Conditions relatives au temps.
Le milieu extérieur étant défini, quelles sont les interactions du système avec lui (contacts ou à distance...) ? Existent-ils des échanges avec l'extérieur (matières, énergies...) ?
Et seulement après, ce qui constitue des hypothèses, quels outils (variables, lois...) et méthodes utiliser pour décrire l'évolution, le mouvement ou l'état du système ?
Et comme dans tous les domaines, la démarche va souvent du plus simple au plus compliqué : du point matériel vers le système de points.
L'étude du premier installe les bases de l'analyse du mouvement ainsi que les lois le régissant.
La complexité des systèmes de points impose des règles de généralisation, des méthodes, ainsi que des outils permettant de construire les extensions possibles aux lois décrivant le mouvement du simple point matériel.
L'arborescence des systèmes étudiés élabore celle des descriptions, des modélisations.
Même si la finalité reste une description unifiée.
Rappel : Le mouvement du point matériel et sa description en mécanique
Un point matériel ou particule élémentaire est l'approximation extrême pour décrire le mouvement d'un corps dans l'espace ; les dimensions des objets étudiés sont négligées par comparaison à l'échelle du mouvement.
Les limites du point matériel ne posent aucun problème, à l'opposé du système de points : selon que les lois sont appliquées à un point, à quelques uns d'entre eux, ou encore à l'ensemble, les interactions avec « l'extérieur » seront différentes et ajustées.
Néanmoins pour des raisons de visibilité et lisibilité des figures, les points matériels (particules) seront quelquefois représentés par des petites sphères de faibles dimensions.
Le repérage du système dans l'espace est effectué selon des règles à établir, souvent déterminées par le mouvement du système, lui-même tributaire de ses symétries.
Bien que le choix des notations soit factuel, dans ce cours les conventions sont les suivantes.
Notations :
Le point matériel est noté
.
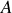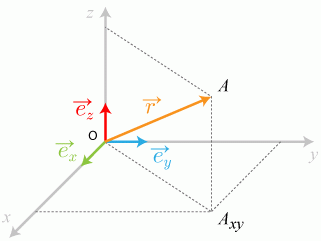
Dans un repère cartésien (
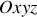) "fixe", la base orthonormée est composée des vecteurs unitaires (
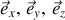), et
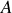est décrit par le rayon-vecteur
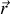(fig.1)
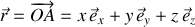
Cependant selon la symétrie de la trajectoire, de la force résultante (contraintes comprises) qui produit le mouvement, d'autres systèmes de repérage et de coordonnées existent.
Ils sont le plus souvent mobiles.
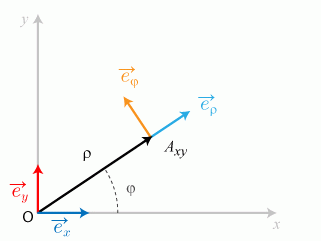
Par exemple, le système de coordonnées polaires (
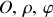) (fig. 2), peut être associé au repérage de la projection du point
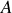, noté
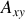, dans le plan
.
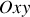Ses vecteurs de base sont (
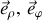) et son rayon-vecteur est
.
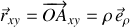Un retour vers la description dans l'espace à
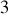dimensions, selon la symétrie du mouvement, utilise
les coordonnées cylindriques (
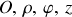) de vecteurs de base (
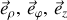) ou les coordonnées sphériques.
Le lien entre les coordonnées polaires et sphériques représentées ci-dessous (fig. 3), notées (
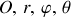) a lieu via la relation :
.
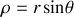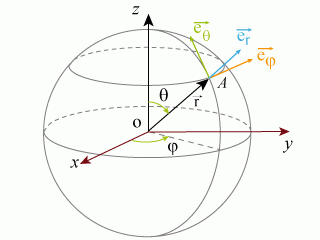
Les vecteurs de base des coordonnées sphériques (
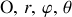) (fig. 3) ont respectivement les directions
de
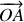, (noté
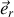), de la tangente au tropique : la parallèle à l'équateur passant par A, (noté
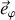pointant vers l'est) et de la tangente au méridien(noté
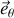pointé vers le Nord géographique).
Tous ces vecteurs unitaires sont centrés en
.
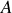Finalement le système de coordonnées intrinsèques décrit les coordonnées curvilignes et courbure des trajectoires(voir la BAO du cours d'électromagnétisme pour des notations plus complètes).
Définition : Généralisation à N points matériels
Pour tenir compte des dimensions spatiales du système mobile étudié, on le supposera, dans un premier temps et en toute généralité, constitué de
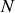particules.
Ce nombre
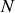peut être fini ou infini, et les particules fixes ou non les unes par rapport aux autres : ceci marque la nuance entre solide déformable et indéformable.
Chaque particule a une masse notée
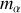, où
.
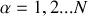Chaque particule
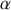est alors repérée en coordonnées cartésiennes par :
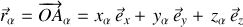
Les lois de la dynamique s'appliquant à chaque particule, les équations sont multipliées d'autant .
Conseil : Gérer la complexité en Physique
La multiplication des inconnues dans le cas de système à grand nombre de particules nécessite une démarche simplificatrice pour continuer l'investigation et apporter quelques éléments d'information sur le mouvement de cet ensemble et/ou résoudre complétement le problème.
La nécessité de mettre en place des méthodes plus globales conduit certes à la réduction de la complexité mais en contrepartie d'une réduction de la généralité des réponses.
Ces méthodes peuvent s'appuyer
sur des particularités des systèmes, géométriques par exemple, ou
sur des pratiques de mesure, la physique étant une science expérimentale, notamment.
En thermodynamique, les mesures de pression, température, composition ou volume, montrent que des informations sur un système sont accessibles sans développer une description incluant chaque particule élémentaire.
Deux voies sont couramment exploitées :
celle du formalisme empirique et phénoménologique (les mesures produisent les lois),
celle de la modélisation statistique laquelle permet d'établir de nouvelles lois, partant de celles microscopiques (par particule) et aboutissant à des grandeurs macroscopiques, nécessaires à des mesures comparatives.
La passerelle entre les 2 voies consiste en une ‘redéfinition' (ou un complément de définition) des grandeurs mesurables.
En thermodynamique, la pression est associée à la moyenne statistique des énergies cinétiques des particules dans le gaz, puis à la température macroscopique si le gaz est parfait ou presque parfait et finalement à son énergie interne. (Chapitre 4)
Fondamental : Le solide, du discret au continu.
La mécanique du solide, un cas particulier du problème à N corps, dispose d'un atout, d'une richesse supplémentaire qui parait à la suite de questions 'en apparence' réductrices : points particuliers, mouvements particuliers...
En effet, lorsqu'elles sont associées à la composition des mouvements (Chapitre 3), les réponses à ces questions décrivent des mouvements généraux.
Ainsi les notions intuitives de continuum, ou de continuité de la matière puis de densité, permettent déjà d'entamer la complexité du système discret.
Une démarche interrogative, alliée à une volonté de simplifier le problème mécanique, peut ainsi être appliquée au corps solide.
Méthode : Existe-t-il des points pouvant jouer un rôle particulier dans le mouvement ?
Le solide peut être d'abord considéré indépendamment de tout mouvement, dans un "état d'équilibre" ou statique (grain 3 sur les solides), ou via ses symétries géométriques.
Pour tout solide indéformable (S.I.), le centre de gravité est un point fixe noté
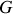(autres dénominations : centre de masse ou CdM, centre d'inertie, barycentre selon l'approche). Il est déduit directement des symétries du système. Il est indépendant du mouvement du solide.
Par exemple, le milieu d'une ligne homogène, le centre d'un disque ou d'une sphère homogène, le point de concours des médianes d'une pyramide triangulaire...
Ce point particulier devient un élément mécanique important qui va apparaître dès les référentiels galiléens (Chapitre 3) avant de décrire le mouvement global du solide dans l'espace.
(Grain 3)
Lorsque les symétries sont visualisées pour le CdM
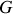, elles le sont également pour les axes dits propres d'un solide, lesquels sont des axes de symétrie dont
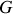est le point de concours.
Selon le solide considéré, des plans de symétrie peuvent également apparaître.
Ces éléments vont jouer un rôle privilégié dans la description des mouvements de rotation notamment.
(Grain 3)
Exemple : Le ballon de rugby
Un ballon de rugby lancé en l'air va décrire une trajectoire dans l'espace entre deux joueurs ; chaque point du ballon va nécessairement décrire ‘une trajectoire' vue des gradins, par exemple ; c'est la translation d'ensemble, globale, qui peut être décrite par le mouvement du CdM.
Mais de plus près, les joueurs peuvent noter les rotations du ballon autour de ses axes de symétrie, rotations qui peuvent être initiées, mais sont moins évidentes à anticiper au moment du contact.
Méthode : Peut-on définir, discriminer des mouvements spécifiques ?
Pour le système indéformable, on pourra donc isoler la translation de chaque point sur la trajectoire, en général curviligne : c'est la "translation globale".
A ce mouvement vont s'ajouter les "rotations locales" autour d'axes de rotation constitués, eux, de l'ensemble des points du solide qui ne tournent pas.
Des référentiels appropriés seront utiles à cette décomposition ou composition de mouvements.
Remarque : Translation circulaire ou rotation
Dans cette formulation, la "rotation de la terre autour du soleil" devient une "translation circulaire" ou faiblement elliptique autour du soleil.
Elle est à dissocier de sa rotation propre autour de son axe (propre de rotation).
Les repères mobiles définis précédemment prennent alors toute leur signification puisqu'ils sont également différenciés pour suivre la translation globale ou permettre de décrire séparément les mouvements de rotation autour des axes des solides.
(Chapitre 3 et grain 3)
